Optimization algorithms execute iterative operations to come up with numerous solutions and then compare those to reach the optimum solution. While there are many sub-types of optimization algorithms, one of the most valuable, useful, and exciting types is Genetic Algorithm.
Data science employs various types of algorithms to solve business problems. These include algorithms like regression, classification, time series, and segmentation algorithms. However, the kind of algorithm that is relatively less talked about but is most crucial as it helps work these other algorithms is optimization algorithms.
Optimization algorithms execute iterative operations to come up with numerous solutions and then compare those to reach the optimum solution. While there are many sub-types of optimization algorithms, one of the most valuable, useful, and exciting types is Genetic Algorithms.
What is Genetic Algorithm?
Genetic Algorithms are heuristic search algorithms that solve constrained and unconstrained optimization problems using the concepts of natural selection – a famous discipline in biological evolution.
To understand genetic algorithms, you first need to understand evolution and its related concepts like natural selection, survival of the fittest, mutation, crossover, etc.
-
Inspired by the concept of evolution
As per biological evolution, every living organism evolves, i.e., adapts to its surroundings and gets better (in terms of survivability and replicating themselves successfully) through evolution.

In a population, due to random alterations in the genes (mutation) during reproduction, certain individuals are more apt to the surroundings than others, i.e., are fitter than others.
Under natural selection, from a population, only the fittest individuals survive or are allowed by the laws of nature to produce offspring (i.e., survival of the fittest).
The offspring, therefore, are often better than their parents as they have inherited characteristics added to their genes that increase their chance of survivability and producing offspring.
The new set of offspring, i.e., a new generation, creates a population that is unique from the previous one due to mutations and the fact that each individual is a recombination of genes of the two parents (crossover).
When this process takes place iteratively in each generation, then at the end, the population consists of the fittest of the individuals.
These concepts of evolution can be applied to search algorithms where you start with a set of solutions to a problem.
In each iteration, the solutions are tweaked, the solutions that performed the best are kept, and the rest are discarded. This process terminates when the maximum number of iterations (generations) is reached, or the optimal/desired solution (fitness level) is achieved.
Key Terminologies
There are specific terminologies in the domain of genetic algorithms that you must know to understand the workings of genetic algorithms properly. The most crucial ones are-
| Population | It refers to the subset of all possible solutions to a problem |
| Chromosome aka. Solution aka. Individual |
|
| Gene | Each variable component is referred to as a gene. Thereby, a collection of genes forms a chromosome |

| Selection | A stage where the optimal solution is selected for the next iteration for breeding (crossover) |
| Crossover | Recombination of genetic information to generate new solutions |
| Mutation |
|
| Allele | Within a particular chromosome, it refers to the value provided to a gene |
| Fitness Function |
|
| Genetic Operators | The genetic operator changes the genetic composition of offspring, ensuring that the offspring is better than the parents |
| Search Space | The search space is where the population is maintained, where each individual is a solution |
What is the Purpose of Genetic Algorithm?
To summarize what genetic algorithm is all about, it refers to an iterative process to find the desired/best solution from a set of possible solutions. Thus,
Searching and optimizing are the two purposes of such algorithms.
The three broad steps to such a type of algorithm are as follows-
- Initialize a random population – P
- Assess the fitness of the population
- Perform the following iterative process until convergence is achieved, where convergence can mean finding the desired or optimal results or reaching the maximum number of iterations –
- Select parents and create offspring through crossover
- Perform mutation in the new population
- Assess the fitness of the new population
Thus, the pseudo-code looks something like-

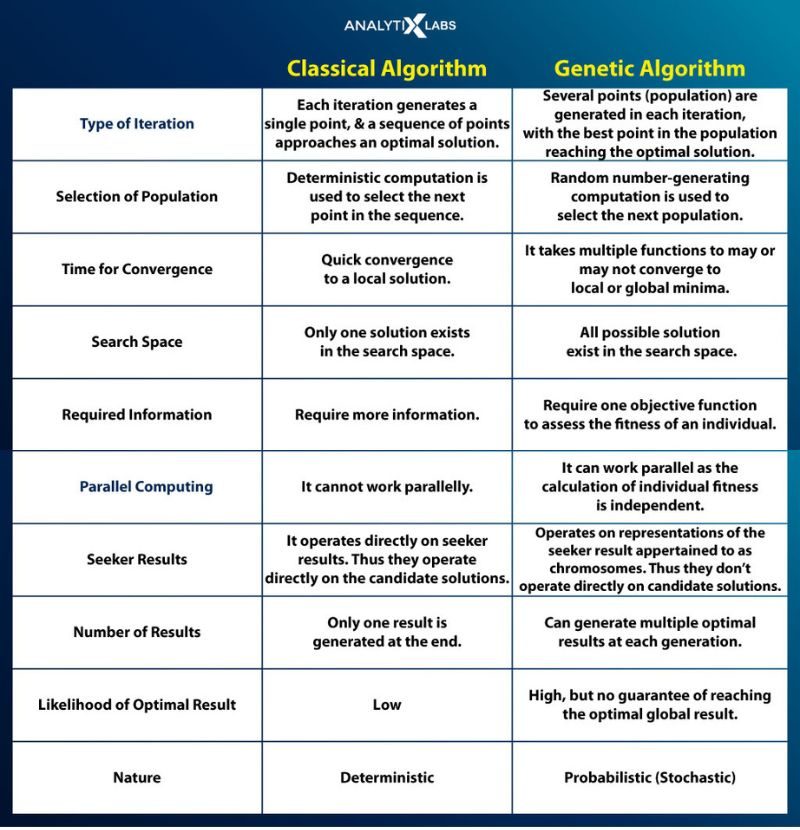
Now that the definition of genetic algorithm is clear let’s dive deep into how genetic algorithms work. However, before doing so, let’s quickly understand how they differ from traditional, i.e., classical algorithms.
Genetic Algorithm vs. Traditional Algorithm
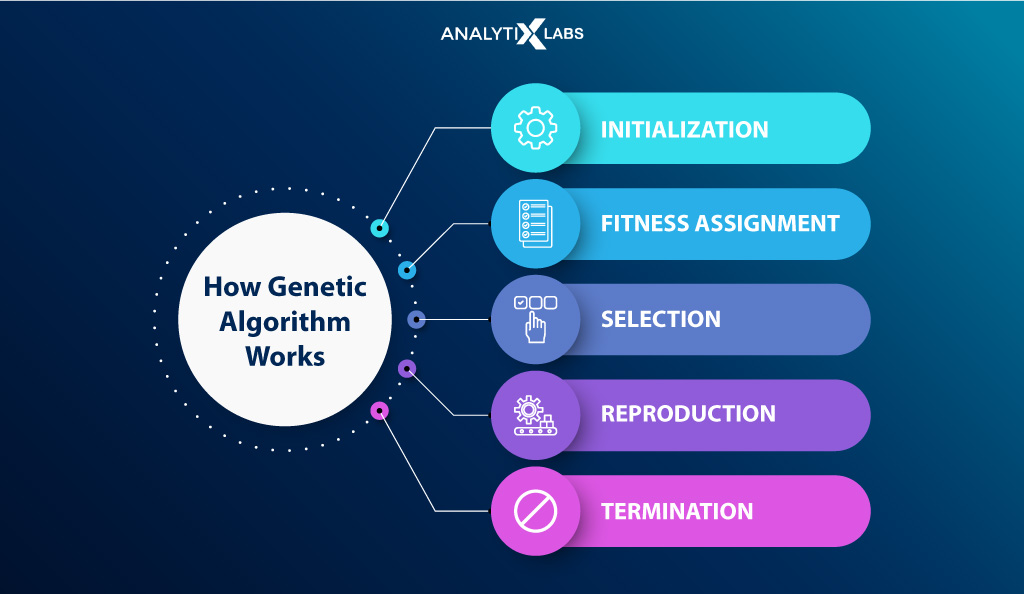
How Genetic Algorithm Work?
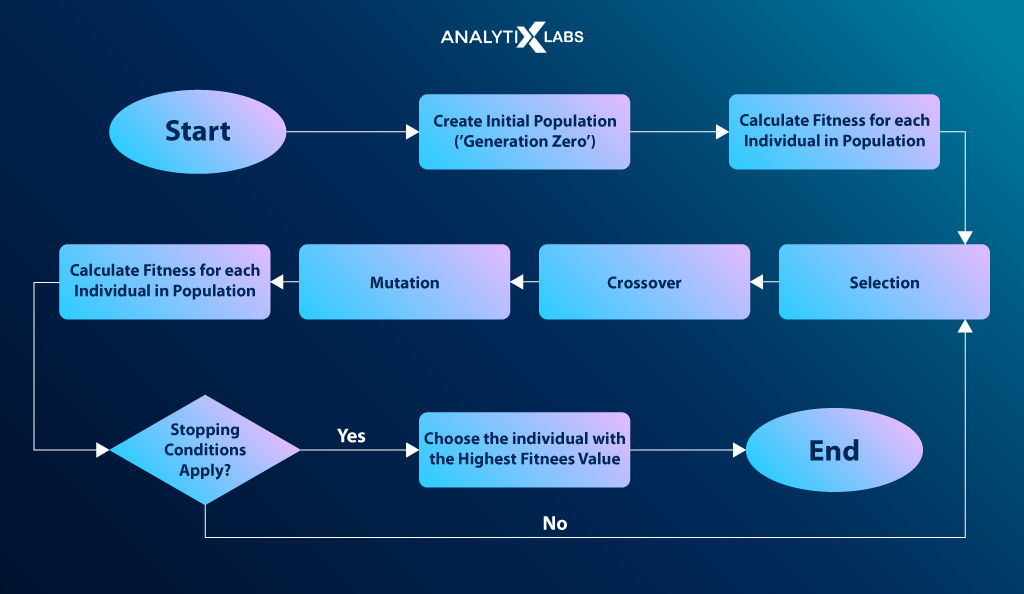
There are broadly six steps in the workings of a genetic algorithm. These include setting up the initial population, determining fitness, the selection, crossover, and mutation phase, and the termination of the process upon convergence. Let’s start with population.
(1) Initial Population
The first step in the process is setting up the initial population, where individuals are provided with a search space.
As discussed earlier, each individual is a possible solution (chromosome) formed by a set of parameters, i.e., variable components (genes). Thus,
A solution (chromosome) is formed when genes are joined into a string.
An individual’s set of genes is represented using a binary string in terms of an alphabet, thereby encoding the genes in a chromosome.
Other forms of representation include –
- Real Value Representation
Using float and real-valued numbers to represent genes.

- Integer Representation
Integers can be used to represent genes. For example, North, South, East, and West are represented by 1,2,3 and 4.

- Permutation Representation
They are typically used when there is order to the elements being represented. For example, the time consumed in distance traveling can be encoded, with 0 representing the lowest and 9 representing the maximum consumed time.

(2) Fitness Function
A fitness function is used to assess an individual’s fitness level. The function returns a fitness score for each individual, indicating the probability of being selected for reproduction.
(3) Selection
The selection of the fittest individuals is based on the fitness score in this phase. Individuals are selected to be parents. The parents are expected to have high fitness scores to reproduce and create better offspring in the subsequent crossover phase.
There are many selection operators out there, such as
-
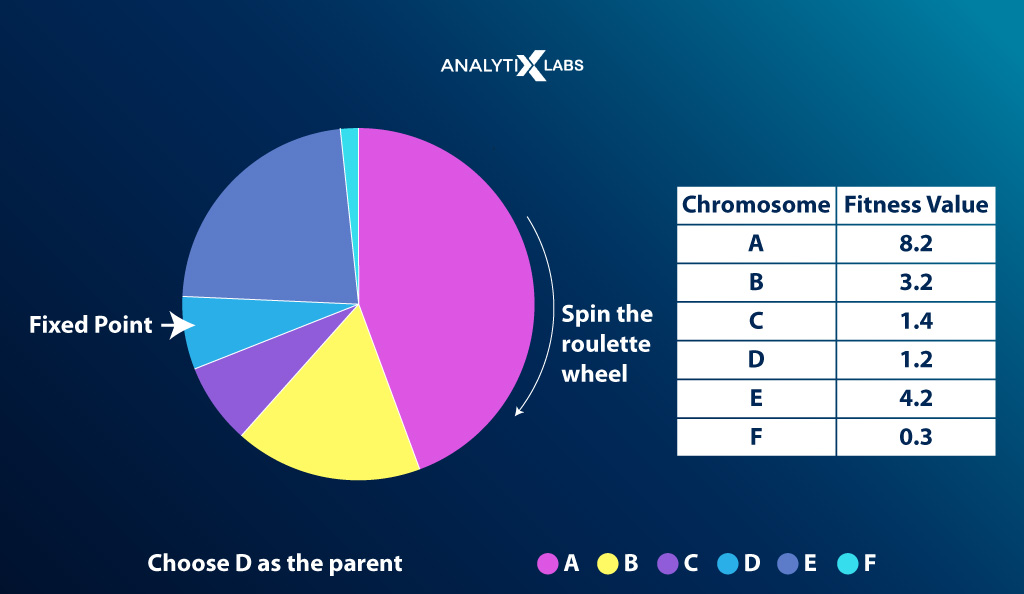
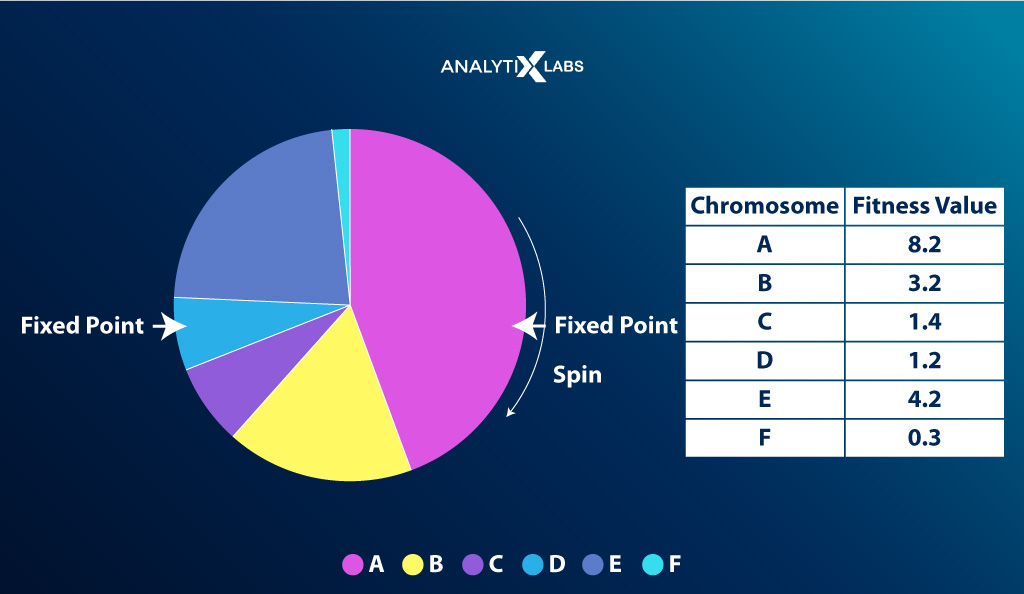
Roulette Wheel Selection
Imagine a wheel is divided into n pies where n = the number of chromosomes. Each individual gets a portion of the circle proportionate to their fitness score. This wheel acts as a roulette wheel with a fixed selection point on the wheel circumference.
The wheel is then rotated, and the region of the wheel that falls in front of the selection point is chosen as a parent. The process is then repeated to find the second parent.
As fitter individuals have a larger pie, they have more chances of making it as a parent.
-
Stochastic Universal Sampling
This method is similar, with the difference being that multiple selection points allow for the selection of parents in a single spin, increasing the chances of selecting highly fit individuals at least once.
-
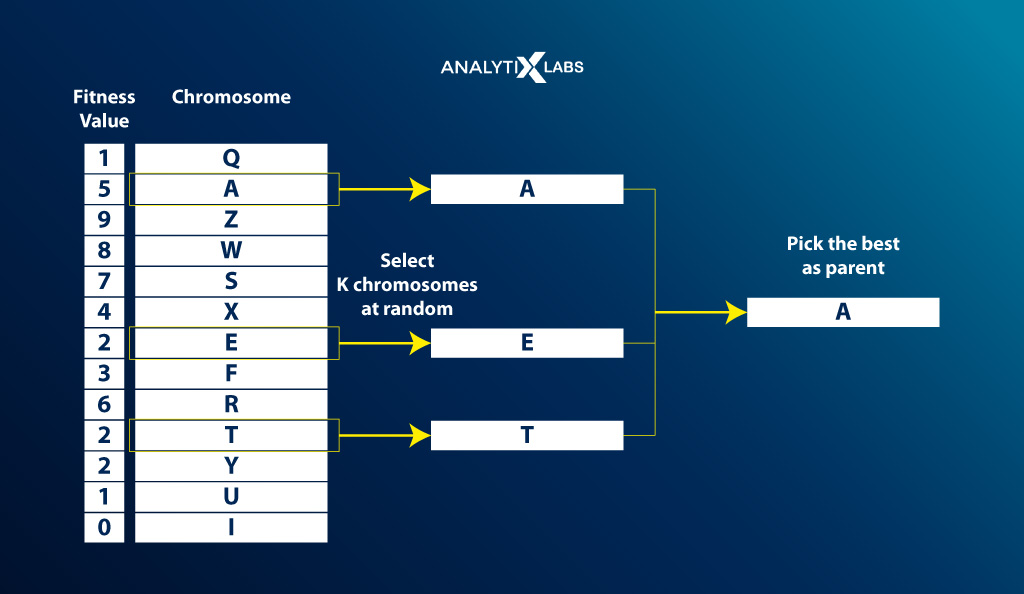
Tournament Selection
K-individuals are selected randomly from the population, and the fittest individual from this group is considered a parent. This step is then repeated to find the next parent.
-
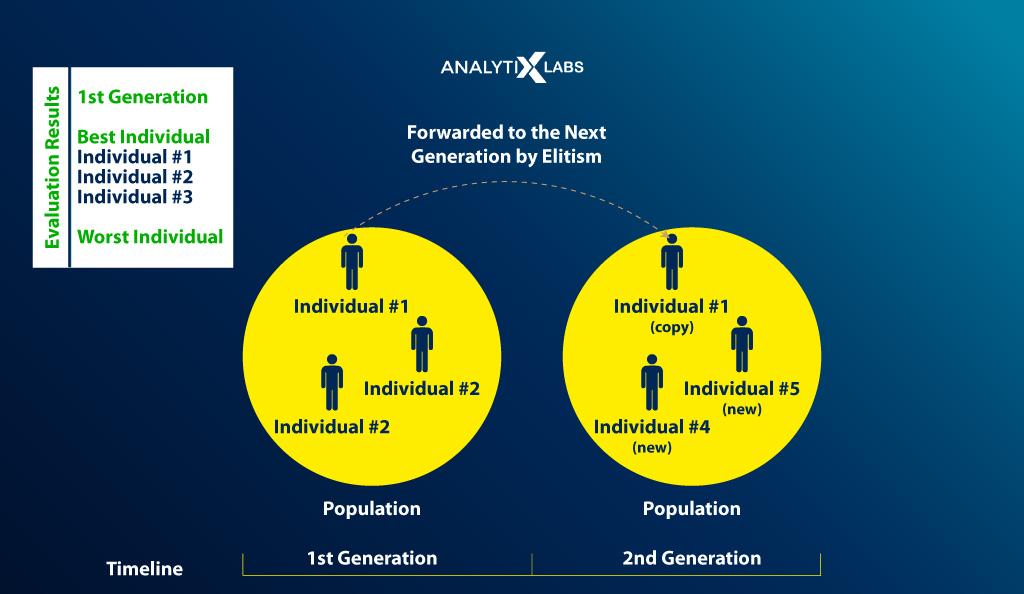
Elitism Selection
Under this selection strategy, a limited number of highly fit individuals are selected to be passed on to the next generation.
Through elitism selection, one can ensure that the best individuals of a generation are available in the next generation, helping you to exploit the promising areas of the search space across multiple generations.
This, in turn, increases the chances of finding the local or global optima result.
This method ensures that good genes are not destroyed due to crossover and mutation. However, the proportion of elite individuals in the population cannot be too high. It will degenerate the population, reduce diversity, decrease chances of exploring new search space, and consequently stall progress.
As one must maintain the required population and diversity, the method is tuned using numerous configurations. One of a configuration of performing elitism include-
- Select the top 10% of the population as the ‘Elite Group’ and allow it to pass to the next generation as it is.
- Select the top 50% of the population to mate and pass offspring to the next generation.
- Select the bottom 50% of the individuals in the ‘Elite Group’ to mate with the non-elite individuals.
-
Random selection
Parents are selected randomly from the population.
Other Selection Operators
There are many more such selection mechanisms with their own merits and demerits, such as
1. Truncation Selection
2. Steady State Selection
3. Ranking Selection
- Linear Ranking Selection
- Non-Linear Ranking Selection
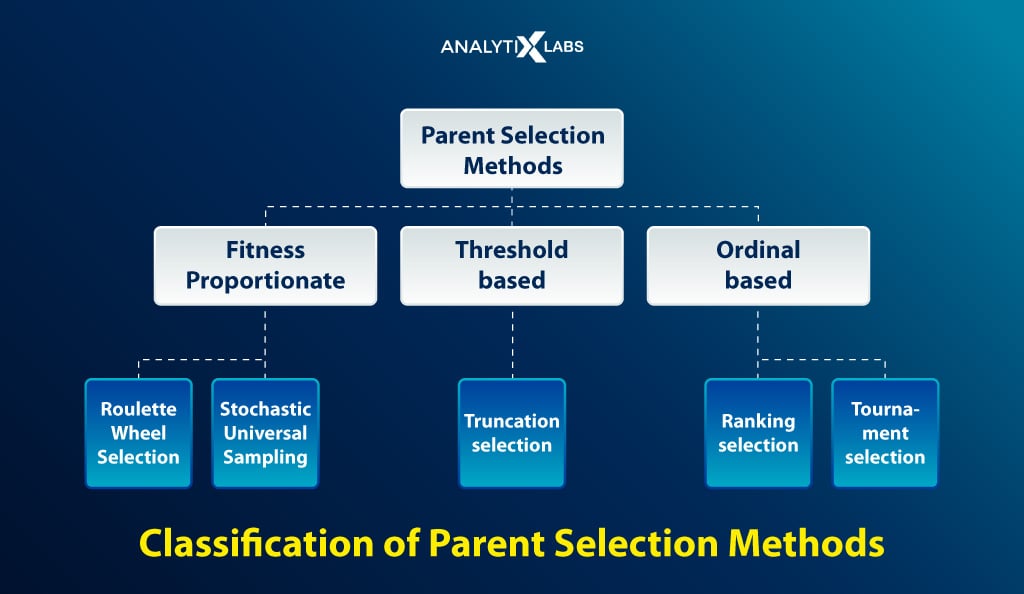
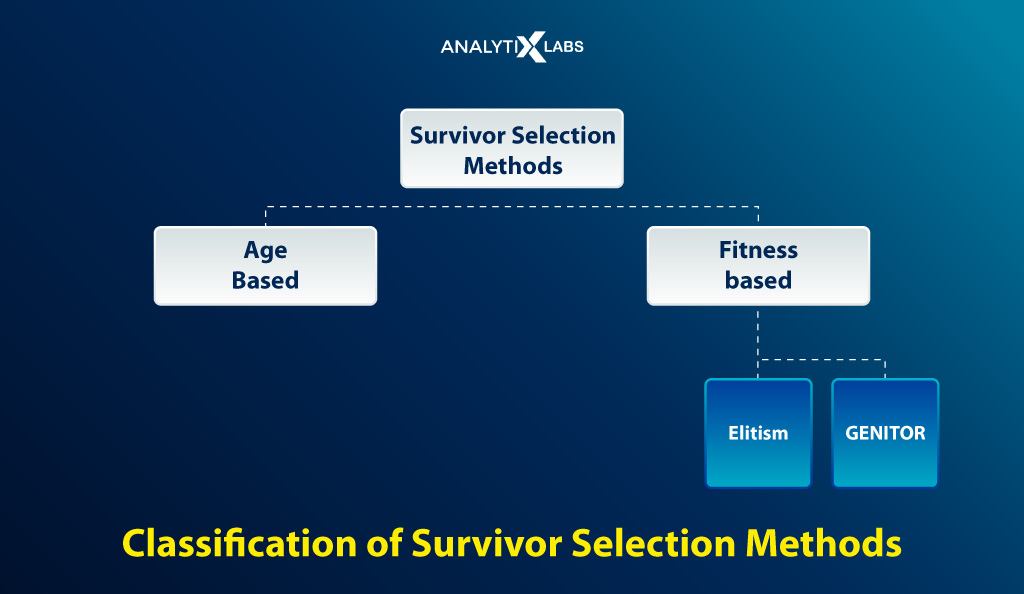
4. Survivor Selection
- Age-Based
- Fitness Based Selection such as GENITOR Selection etc.
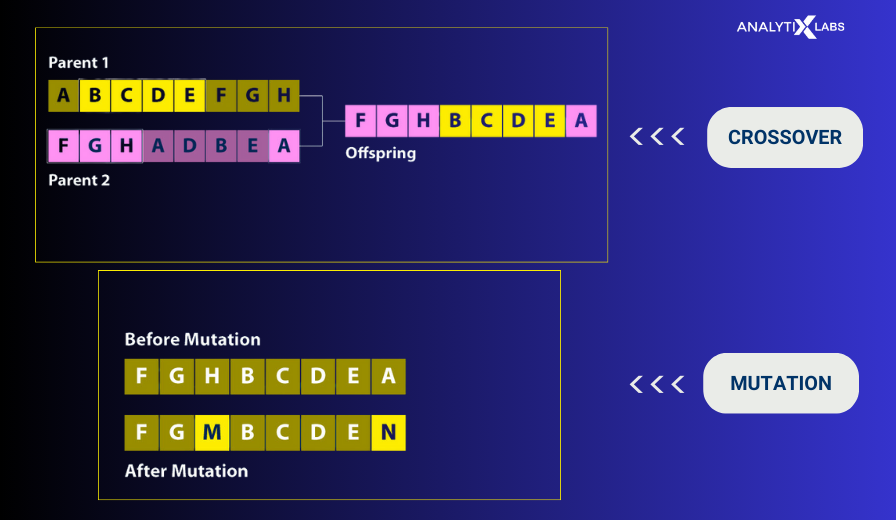
(4) Crossover
The most crucial phase is Crossover, where random point(s) is/are chosen within the parents’ genes to mate and create offspring. There are multiple operators for performing crossover, such as
-
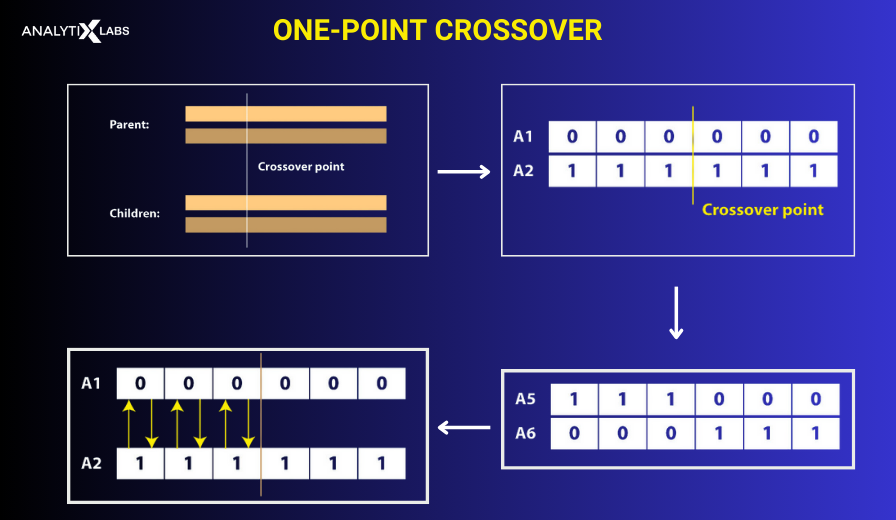
One Point Crossover
One point or single point crossover operator is where a single point is selected that is used by parents to exchange genes.
- Let the parents be A1 and A2, creating offspring using a single-point crossover mechanism with the crossover value being 3.
- Exchange of genes till crossover point is reached.
- The two new offspring are A5 and A6.
-
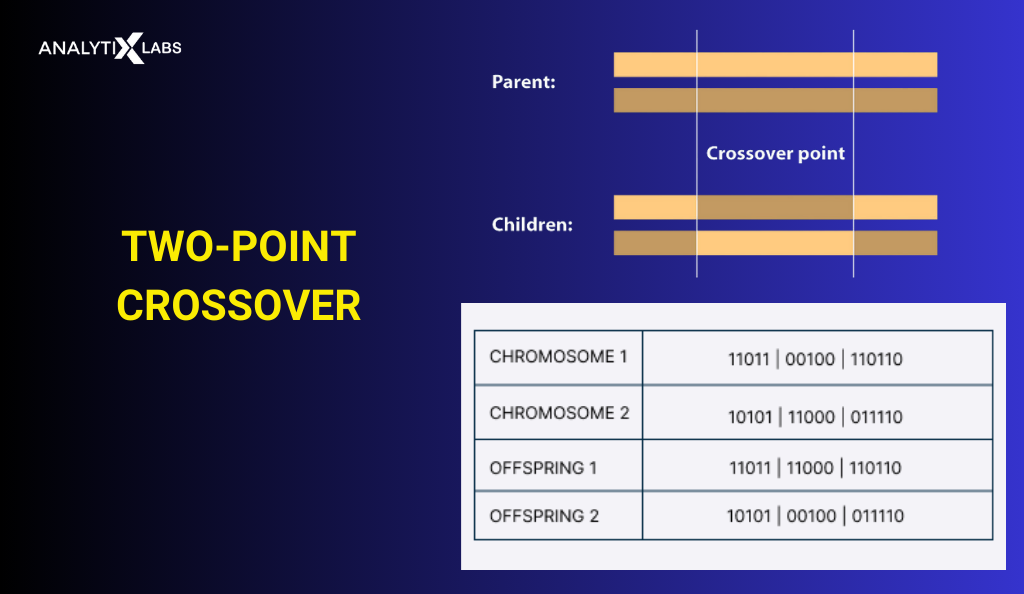
Two Point Crossover
It’s a particular case of the K-point crossover technique with K=2 as two random points are used in the chromosome to exchange the genetic material.
-
Uniform Crossover
Each bit in the chromosome of the offspring is selected randomly from one of the corresponding genes of the parent chromosomes.

Other Crossover Operators
There are many more such crossover operators, such as
- Livery crossover
- Inheritable algorithms crossover
- k-point crossover
- Multi-point crossover
- Half-uniform crossover
- Uniform with mask
- Shuffle
- Matrix
- Three parent
- Linear
- Single arithmetic
- Partially mapped
- Cycle

(5) Mutation
To maintain genetic diversity and prevent premature convergence, genes of certain offspring are mutated, i.e., edited with a low random probability. There are multiple methods of mutation, such as –
-
Flip Bit mutation
Some of the bits in the bit string are flipped at random.

-
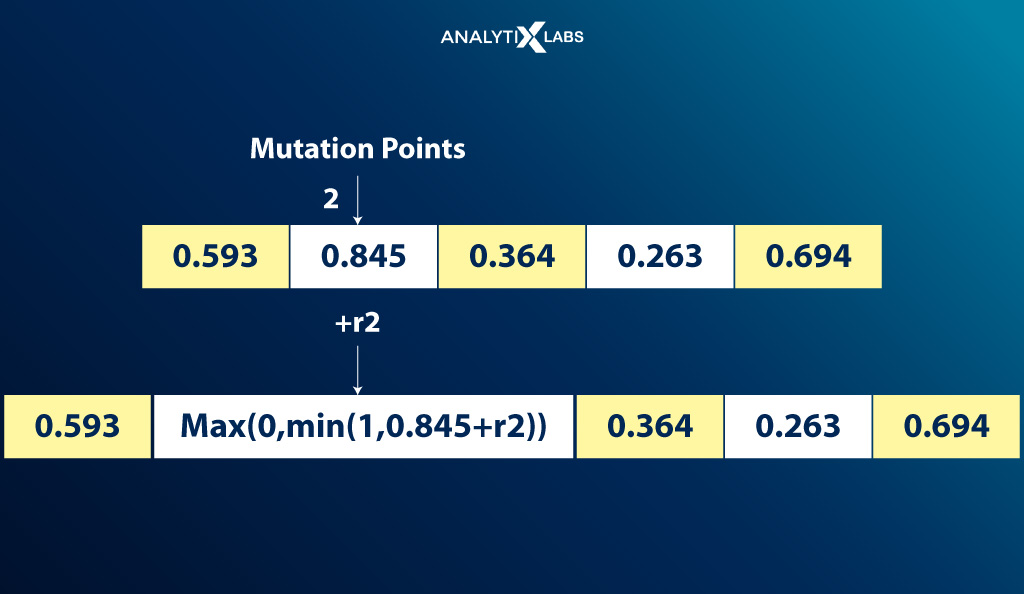
Gaussian Mutation
The Gaussian error function is used where a random value from the Gaussian distribution is used for mutation.
-
Exchange/Swap Mutation
Two positions at random are selected on the chromosome to interchange the values.

(5) Termination
The last step is when the process of selection, crossover, and mutation terminates. This is typically achieved in two ways-
- Reaches the maximum number of generations
The maximum number of iterations set by the user is reached.
- Reaches a sufficient level of fitness
The required or optimum solution is reached. This is typically determined by ensuring that one or more individuals in the population have achieved the desired fitness score and that the offspring are not significantly different and better than the previous generation.
Running a Genetic Algorithm in Python
To put whatever you have read so far in perspective, let’s perform genetic programming by considering a problem and solving it using the mechanisms of genetic algorithms.
While one can write Java genetic algorithms or C++ genetic algorithms, writing and using genetic algorithms in Python is relatively easier.
For example, the desired solution is to have a string ‘I study @ AnalytixLabs’. We are tasked to start with random strings having the same length as the desired one and reach the solution.
Let’s look at the flowchart below and decide the architecture we will follow for the algorithm.
- Acceptable Genes: The acceptable genes are A-Z, a-z, 0-9, and other commonly used symbols. A string of all these characters (genes) will be a plausible solution (chromosome).
- Population: The population will be set to 100, i.e., in any given generation, the number of chromosomes will be 100.
- Fitness Function: The fitness function will be such that the fitness score will be the number of characters in a chromosome that does not match the solution. Therefore, 0 will be the desired fitness score.
- Selection: Elitism selection method with the following configuration-
- The top 15% of the population is considered elite and selected to move to the next generation.
- The top 50% of the population will be selected for crossover and considered for mutation to create offspring for the next generation.
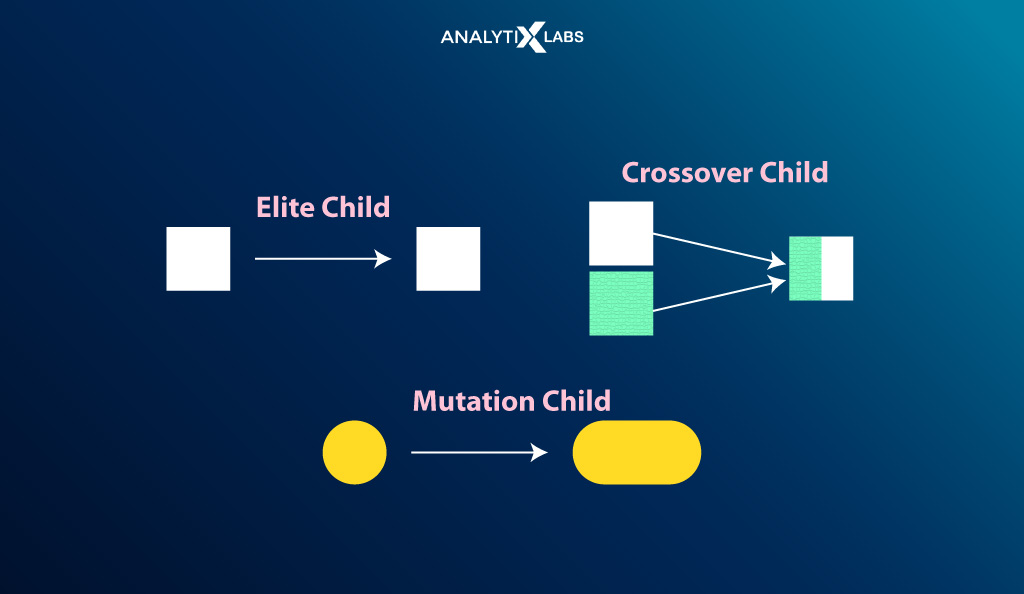
- Crossover: Random probabilities pull the genome from the first and second parent.
- Mutation: Flipping a random gene in the chromosome.
- Termination: The process terminates only when the desired solution is reached, i.e., a chromosome in the population reaches a fitness score of 0.
Let’s now have a look at the code.
- Importing the library –‘random’ to perform various operations
# Importing random library to create and select random bits
import random
- We now perform genetic programming by creating a class ‘Chromosome’ where various functions are written to define the initialization, mutation, crossover, and fitness function mechanism.
# Creating a class that performs initialization, mutation, crossover, fitness score calculation
class Chromosome(object):
# initializing class
def __init__(self, chromosome):
self.chromosome = chromosome
self.fitness = self.fittness_score()
# MUTATION MECHANISM: a function that selects a random gene to be used for mutation
@classmethod
def genes_mutated(self):
global genes
random_gene = random.choice(genes)
return random_gene
# a function that creates a chromosome
@classmethod
def create_chromosome(self):
global Solution
genome_len = len(Solution)
return [self.genes_mutated() for i in range(genome_len)]
# CROSSOVER MECHANISM: a function that can perform crossover (mating) to produce offspring
def crossover(self, second_parent):
# creating an empty chromosome for offspring
child_chromosome = []
for genome_first_parent, genome_second_parent in zip(self.chromosome, second_parent.chromosome):
# creating random probabilities
prob = random.random()
# crossover such that if prob is less than 0.20, pull gene from first parent
if prob < 0.20:
child_chromosome.append(genome_first_parent)
# crossover such that if prob is between 0.20 and 0.90, pull gene from second parent
elif prob < 0.90:
child_chromosome.append(genome_second_parent)
# perform mutation in other cases by inserting random values
else:
child_chromosome.append(self.genes_mutated())
# generating the offsprings
return Chromosome(child_chromosome)
# FITNESS FUNCTION: creating a function that can calculate fitness.
# The fitness function returns the fitness score for each chromosome such that it indicates the number of
# characters in a string that do not match the solution string. i.e., lower value means better
def fittness_score(self):
global Solution
fitness = 0
for xx, yy in zip(self.chromosome, Solution):
if xx != yy: fitness+= 1
return fitness
- Setting up various parameters to run the algorithm.
# setting the number of chromosomes to be there in every generation
pop_size = 100
# setting all the acceptable values for creating genes
genes = '''ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz 0123456789, !-[]{}().;:_=&"#%/\?@~$'''
# setting the required solution
Solution = "I study @ AnalytixLabs"
# setting the first generation
generation = 1
# setting default value of 'solution_found' as False. Useful when moving to new generation.
solution_found = False
# creating an empty population to start the process
population = []
- Running the algorithm using the various attributes of the class ‘Chromosome’.
# creating initial population
for i in range(pop_size):
genome = Chromosome.create_chromosome()
population.append(Chromosome(genome))
while not solution_found:
# sorting the chromosomes in the population in increasing order of fitness score
population = sorted(population, key = lambda x:x.fitness)
# TERMINATION: Setting termination mechanism
# if a chromosome has 0 fitness score (best) then we know that we have reached to the desired solution
# and can break the loop, if not then generate new offspring for new generation
if population[0].fitness <= 0:
solution_found = True
break
new_generation = []
# SELECTION: Performing selection using Elitism selection method.
# 15% of fittest population is selected for the next generation
x = int((15*pop_size)/100)
new_generation.extend(population[:x])
# CROSSOVER & MUTATION: Performing crossover on 50% of the fittest population
x = int((85*pop_size)/100)
for _ in range(x):
first_parent = random.choice(population[:50])
second_parent = random.choice(population[:50])
child = first_parent.crossover(second_parent)
new_generation.append(child)
# replacing population with the new generation
population = new_generation
# printing the fittest chromosome there in the population of the current generation
print("Generation Number: {}\tSolution: {}\tFitness Score: {}".\
format(generation,"".join(population[0].chromosome),population[0].fitness))
# moving to next generation
generation += 1
# printing the fittest chromosome in last generation along with the fittness score
print("Generation Number: {}\tSolution: {}\tFitness Score: {}".\
format(generation,"".join(population[0].chromosome),population[0].fitness))
The output shows that the best-performing chromosome in the first few generations returns an unintelligible solution.
As the generations progress, the fitness score gets better (lower), and the solution tends to reach the optimal one. The process finally terminates when the required fitness level is achieved.

If you want to know the languages, you must try writing C++ genetic algorithms or Java genetic algorithms, as many genetic algorithm ideas are available in these languages.
I hope this detailed discussion on the inner workings of genetic algorithms has helped you understand this domain better. It’s, therefore, high time to delve into the merits and demerits of using such an algorithm.
Advantages of Genetic Algorithm
There are multiple advantages to using genetic algorithms, such as
- Genetic algorithms are easy to understand as the concept uses the common principles of school-level evolutionary biology.
- The algorithm is separate from the application, making it highly agile.
- The accuracy in such an algorithm evolves (through generations); thus, you can find the required result with enough time and computation power.
- The computation of genetic algorithms can easily be distributed as the working are inherently parallel.
- Genetic algorithms don’t require derivative or auxiliary information as they obtain the fitness score from the objective function.
- It can optimize various functions, such as discrete functions, continuous functions, mixed continuous/discrete problems, objective problems, etc.
- A significant advantage of genetic algorithms is that they can solve problems from various domains, from engineering and medicine to finance and logistics.
- Genetic algorithms that belong to the family of biological algorithms can also solve highly complex problems that are otherwise too difficult to solve using traditional optimization algorithms.
- It has a high probability of finding the global minima and not getting stuck to local minima.
- Genetic algorithms don’t need derivative information.
- Other advantages include successfully working with problems with multiple local optima, the objective function is not smooth, many parameters need to be optimized, or the objective function is noisy or stochastic.
Limitations of Genetic Algorithms
While there are many significant advantages of using genetic algorithms, there are several disadvantages too that you must keep in mind when using such an algorithm, such as-
- It’s highly computationally expensive to run such an algorithm as it needs to look at the search space and examine multiple permutations and combinations before it reaches the desired result.
- Given its stochastic nature and the need to perform multiple iterations to find the solution, the genetic algorithm can be time-consuming as it can take much time to converge.
- While the algorithm is efficient in solving complex problems, it is counterproductive and inefficient in solving simple problems.
- While understanding the concept is easy, implementing the genetic algorithm is challenging and sometimes is more of an art. If not appropriately implemented, the algorithm can converge to a non-optimal solution.
- While less information is required by the user about the problem, this advantage gets offset due to the difficulties in designing the objective function, selecting suitable operators, and getting representation.
- There is no guarantee of the quality of the results generated by such algorithms.
With all the advantages and disadvantages, the genetic algorithm can and is being used in multiple domains and areas. The primary application areas of genetic algorithms are discussed in the next section.
Application Areas
Multiple genetic algorithm examples illustrate the types of problems, domains, and areas where implementing the genetic algorithm can yield great results. These include the following-
- Machine Learning: Genetic algorithm in machine learning helps in tuning multiple hyperparameters.
- DNA Analysis & Medical Science: Given how many genetic concepts such algorithms use, it’s no surprise that they are heavily used in DNA analysis, helping medical professionals to establish DNA structure using spectrometric information.
- Neural Networks: Genetic AI refers to using genetic algorithms that support optimizing neural network pipelines, inheriting qualities of neurons, finding the best combination of parameters for a network, etc.
- Clustering: Clustering can be used to find the optimal center point of clusters.
- Image Processing: Helps in image segmentation and other image analysis-related problems requiring optimization.
- Wireless Sensor Network: Genetic machine learning can be used to simulate sensors and use fitness functions from the algorithm to optimize operational stages in a WSN.
- Traveling Salesman Problem and Vehicle Route Optimization: Find the optimal way to cover the distance between two points in real time.
- Financial Markets: Genetic algorithms are used to find the combination of parameters that can affect the market rules and trades.
- Task Scheduling: The algorithm can describe the optimal schedules based on specific constraints.
Other genetic algorithm examples include-
- Data Mining
- Multimodal Optimization
- Transport and Logistics
- Aircraft design
- Economics
- Businesses Looking to Maximize Profit
- Robotics
- Mechanical Engineering Design
- Manufacturing System
- Mutation Testing
- Signal Processing
- Code Breaking
- Learning Fuzzy Rule Base
Before we conclude the discussion on genetic algorithms, let’s address a common question: why not just use gradient-based algorithms instead of genetic algorithms? There are multiple reasons for this, as discussed next.
Why use Genetic Algorithm over a Gradient-based Algorithm?
While the gradient-based methods have proven to be valuable time and time again, there are certain limitations to them that make using genetic algorithms enticing. The crucial limitations include the following-
- Gradient-based optimization algorithms require continuous derivable objective functions, whereas direct search algorithms like generic algorithms can work with non-continuous objective functions and domains.
- Gradient-based algorithms are less robust as they depend strongly on the starting point, while genetic algorithms don’t.
- Another failure of gradient-based methods is that they are susceptible to numerical noise, whereas genetic algorithms aren’t bothered by derivatives approximations or any numerical noise.
- Lastly, the gradient-based methods seem to have limited success when dealing with problems with multiple local optima, and genetic algorithms are unfazed by such issues.
Conclusion
In conclusion, if you are dealing with complex problems, genetic algorithms can be an efficient and even a fast alternative. The algorithms belonging to the family of evolutionary biological algorithms are much more unique and intelligent than other traditional and random search algorithms.
FAQs:
- What are the three stages of a genetic algorithm?
The three stages of the genetic algorithm are as follows-
- mutation – random gene alterations
- crossover – swapping genetic material
- selection – only the fittest survive
- What is a genetic algorithm in AI?
Genetic AI algorithm refers to using genetic algorithms to solve complex problems undertaken by AI by aiding in optimizing neural networks.
- What is the use of genetic algorithms?
Genetic algorithms are typically used to search results and find optimal solutions to problems that are usually highly complex and tough to represent. Genetic algorithms in machine learning and AI have become increasingly common.
I hope this article gave you an in-depth understanding of genetic algorithms and has given you the confidence to explore this field of ML and AI on your own. If you want to learn more about such fields, contact us.




![Deep Learning Interview Guide: Top 50+ Deep Learning Interview Questions [With Answers]](https://www.analytixlabs.co.in/blog/wp-content/uploads/2021/11/1-8.jpg)



