Activation Functions In Neural Networks – Its Components, Uses & Types

The activation function in neural network is responsible for taking in the input received by an artificial neuron and processing it to achieve the desired output.

The advent of artificial intelligence has stirred up a revolution that is hard to ignore. Scenes from Mission Impossible or Heart of Stone or as early as Star Trek – all are now extremely believable because that’s how AI has penetrated our daily lives. AI has been around since the 1950s, but only recently have we come to a full realization of its power.

There are many reasons for this, but the most crucial ones include innovations like backpropagation and the dramatic increase in computation power due to increased memory, GPUs, cloud computing, etc. However, to understand neural networks, you need to have the answer of “what is activation function“.

You can define it as a statistical or machine learning algorithm employed by a model where certain activation functions (like the sigmoid function in a neural network) work like a logistic regression algorithm. In contrast, others might work similarly to some other algorithm. 

Understanding what is activation function neural network is easier if you first focus on a few related aspects.

This article will help you understand the use of activation function in neural network, the types of activation function in neural network, their components, and other related concepts.

Let’s start by understanding the  different neural network components .

Neural Network Components

To understand activation functions in ANN and their role in neural networks, you first need to have a certain level of understanding about artificial neurons.

Understanding Human Neuron

AI-powered program/software is any program powered by an ‘artificial neural network’ that performs ‘deep learning’ using ‘artificial neurons’.  To comprehend artificial neurons, you need to understand how human brain cells- neurons work as the artificial ones are based on them. 

Look at the human brain cell ‘neuron’ below.

The main components of the cell are –

1. Dendrites
2. Nucleus
3. Axon
4. Axon terminal

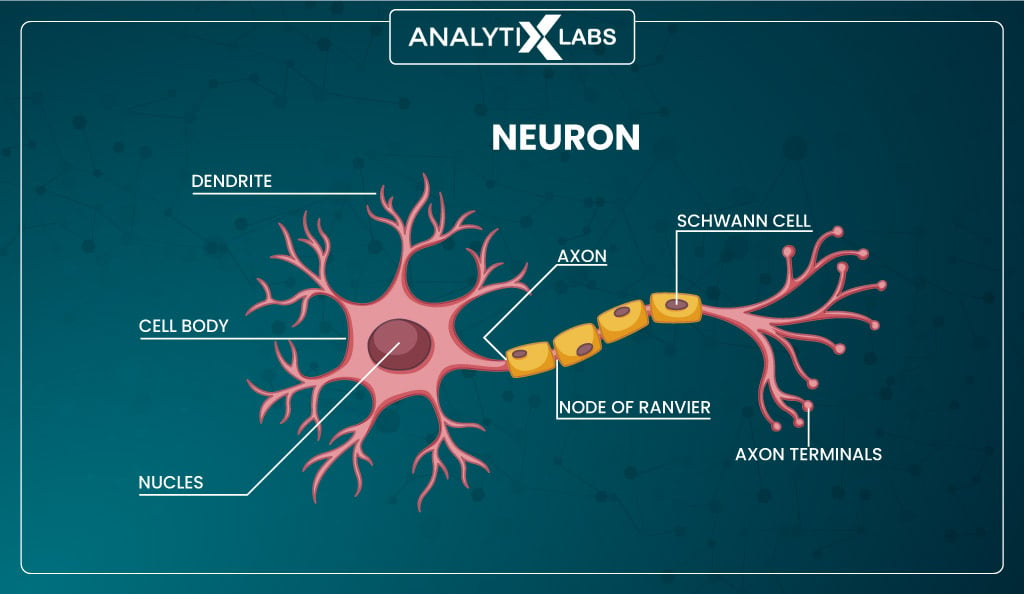
Suppose your hand touches a hot surface.

This causes the fingers to feel the heat which turns this into an electric signal that passes to the brain. The brain cell–neuron receives this signal through the dendrites and passes the signal to the nucleus. The nucleus processes the signal and is predisposed to fire or not fire an electric signal based on the intensity of the received signal.

 Suppose the nucleus gets overwhelmed by the strong incoming signal.

 In that case, it fires an electric signal that passes to the axon that transfers the signal from the soma (cell body) to the axon terminal, where the synapses pick up the signal and pass it to the dendrites of the connected neurons.

Understanding Artificial Neuron

The same concept of neurons is applied mathematically to solve various problems. Here the neurons are artificially created where the input features are the signals the neuron receives.

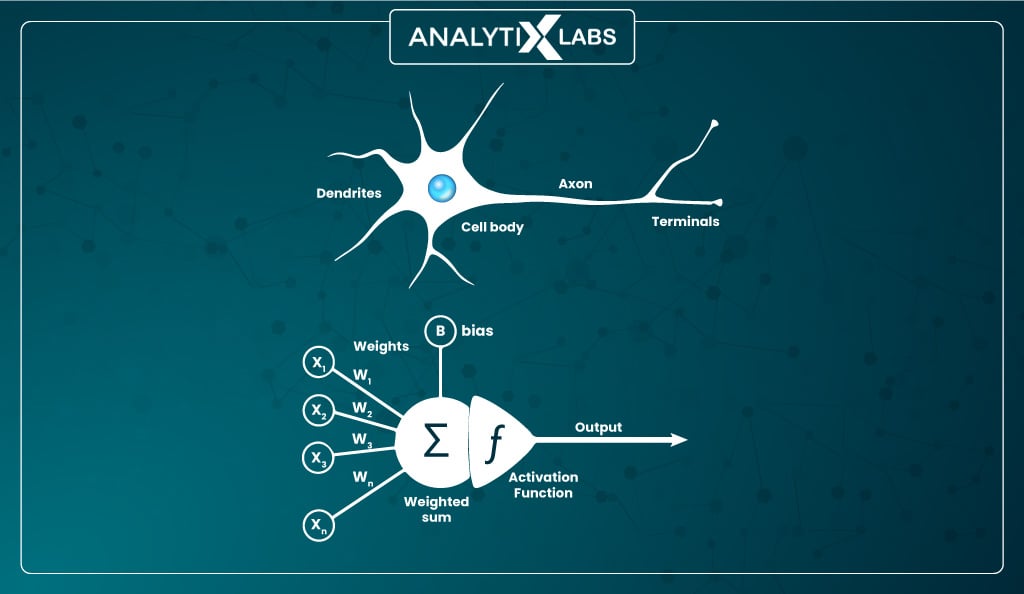
The value of the weights (multiplied by the values of the input feature) determines the strength of the signal. A ‘bias’ value is also added to the node along with the input, which acts as an additional weight determining how easy it would be for the ‘incoming signal’ to pass through the ‘nucleus’.

The node acts as the nucleus, which either generates an output or doesn’t. If some output is generated, it is passed to the attached next neuron or set of neurons to form a hidden layer.

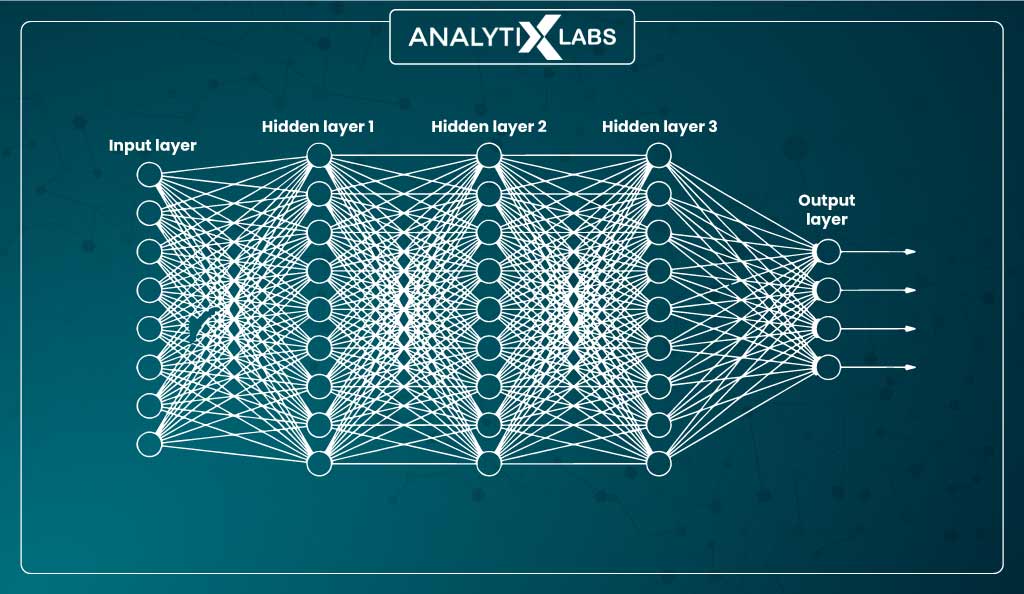
An artificial neural network (ANN) can comprise multiple hidden layers, each with one or more artificial neurons. The users are exposed to just the input layer that receives the values from the features and the output layer that returns the result hence making  the other layers ‘hidden’, giving them the name ‘hidden layers.’

Thus the three main components of an artificial neural network are: 

1. Input layer
2. Hidden layer(s)
3. Output layer

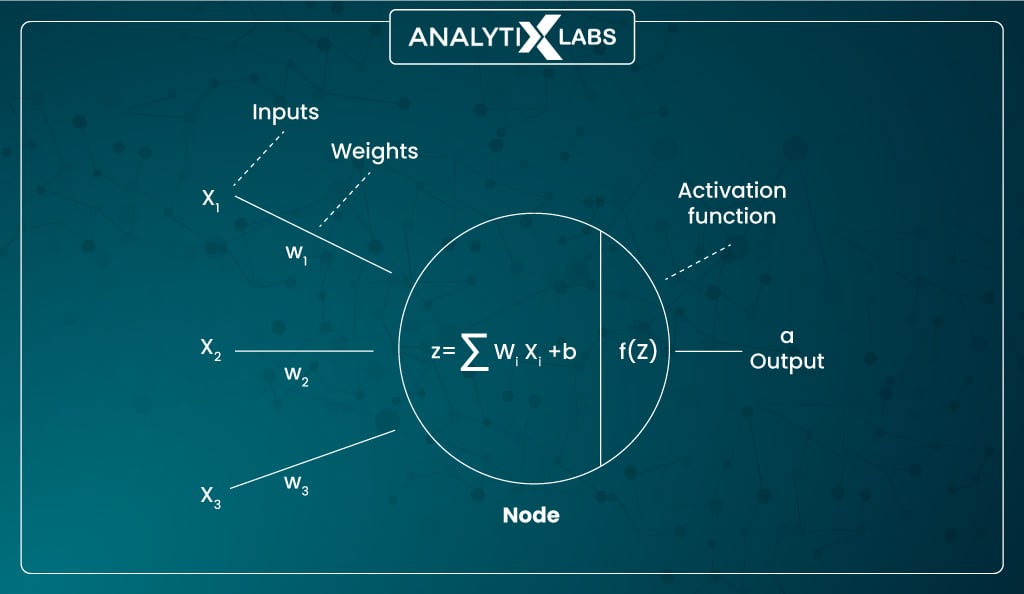
Let us now try to understand the role of an activation function in deep learning, i.e., in a neural network.

What is Activation Function in Neural Network?

The node is where the ‘input signal’ (the values of the input features) and the weights and biases they are multiplied with are summed. This is where the activation function comes into play. It converts this summed weighted input into an output value that is then passed to the next attached neuron or set of neurons, i.e., the next layer.

Therefore, it’s the activation layer that is responsible for making the nodes ‘fire’. It processes the input, returns an output propionate to the quantum of the received signal, checks if the output is crossing the threshold, and if it does, then allows the output to go the neurons of the next attached layer. Hence, the activation function plays a crucial role in an artificial neuron. 

However, the question remains unanswered: using the activation layer, i.e., the multiple activation functions in neural networks.

What will happen if we do not use the node’s activation function and pass the summed weighted input to the next layer?

Let’s find out.

Purpose of Activation Function in Deep Learning

Let’s understand the purpose of the activation function in deep learning with an example. Suppose we have two inputs, x1 and x2, having values 10 and 20. The weights assigned to them are w1 and w2, respectively, with their values being 0.4 and 0.8. The value of bias b0 added to the node is 0.3.

Now when all the values enter the node, the node processes them in the following way-

x1b1 + x2b2 + b0
making the output generated by the node to be-
(10*0.4) + (20*0.8) + 0.3 = 20.3

Note: The calculation here is similar to a linear regression algorithm. 

Now imagine a neural network with hundreds of such neurons without having any activation function.

 In such a scenario, every neuron will act as a linear regression model, transforming all the input using the weights and biases. The eventual outcome would be that all layers would behave similarly, and there would be no addition to the accuracy no matter how many neurons and hidden layers are in the network, as the combination of two linear functions is a linear function.

Therefore, the lack of activation function in the neurons will render the networks unable to solve complex problems that are typically non-linear, and the whole network will function like one big linear regression model.

  Now that we have discussed non-linear problems let’s understand why differentiation is used in neural networks, what linear and non-linear activation functions are, and how they affect the derivation capability of the network. 

Why Derivative/Differentiation is Used?

To understand the need and use of differentiation in neural networks, first, you must know the concept of feedforward and backward propagation.

In feedforward propagation, the flow of information occurs from the input to the output layer, i.e., in the forward direction.

The input is used by some intermediate function in the hidden layer to calculate the output. The issue with the method is that there is no mechanism to make the network better by itself, and this is where backpropagation comes into play.

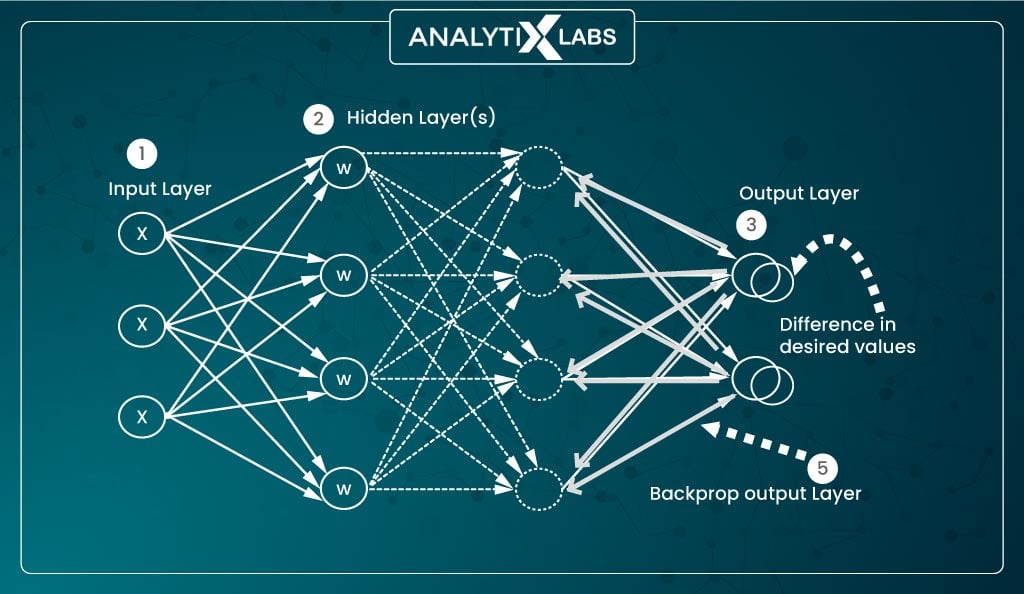
Backpropagation refers to the repeated and iterative adjustment of weights and bias values to minimize the cost function, which is the difference between the actual and desired output vectors.

The information in the network during backpropagation flows from the output layer towards the input layers, whereby the gradient of the cost function determines the quantum of adjustment of the weights and biases other parameters of the activation function.

The activation function in ANN needs to be differential because the concept of differential is used to improve the network.

The differential here refers to calculating changes in y with respect to the changes in x. During backpropagation, differentiation is used to calculate the change in error with respect to parameters like weights ad bias.

If the activation function is not differential, then no form of gradient descent can occur, causing the network to remain as it is and not adjust itself to reduce the error.

Also read: A Detailed Guide on Gradient Boosting Algorithm (with Examples)

Linear vs. Non-Linear Activation Function

As discussed earlier, the hidden layers need to have a non-linear activation function so that the complex problem can be solved and the network doesn’t act like a linear transformer.

Let’s understand all such types of activation function in neural network.

• Linear activation function

Mathematically represented as-
Linear
f(x)=x

The linear activation function is also called an ‘identity function’ or ‘no activation’ because the output is always proportional to the input when using such a function.

Thus, such a function provides you with the weighted sum of the input and technically returns the value fed into the network.

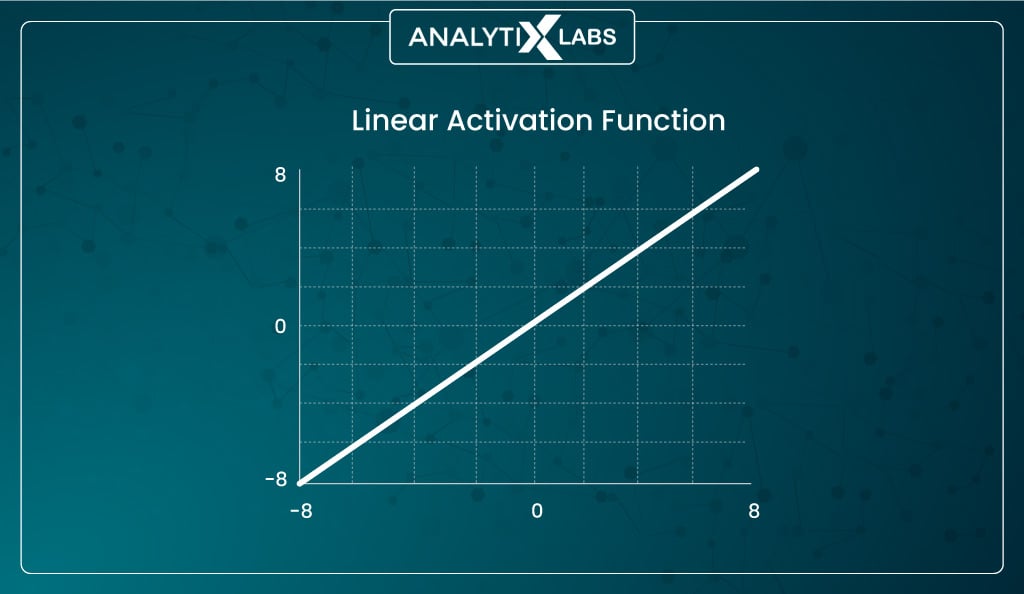
The primary issue with such a function is that no form of backpropagation can occur as derivation is performed during backpropagation to reduce cost. The issue with the linear activation function is that the derivate of the linear function is constant that has no relation to the input x.

Also, as evident in the previous discussion, a network where the activation function in hidden layers is linear causes all the hidden layers to collapse, no matter how many there are, into a single layer performing just the linear transformation. Hence it destroys the whole advantage and purpose of hidden layers.

• Non-linear activation functions

Of the many activation functions in neural networks, the non-linear type is the most powerful. The non-linear functions, in turn, are much more significant than the linear functions as they can create a complex mapping between the input and output.

They are also very crucial for neuron activation. Unlike linear regression, backpropagation is possible here as the derivative function gets related to the input, and it becomes possible to identify the weight that, upon adjustment, can provide better results.

Also, stacking multiple hidden layers yields results as output becomes a non-linear combination of the input. Therefore, non-linear activation functions are always used in the hidden layers of a neural network.

There are many such non-linear activation functions discussed in the next section.

• Binary step function

Mathematically represented as:

Another important activation function for you to know is the binary step function. The binary step function uses a threshold that decides whether the neuron should fire, i.e., neuron activation.

Such a function checks whether the input to the activation function is above the threshold. If the input doesn’t cross the threshold, the neuron is deactivated and doesn’t function, whereas the next layer considers the output if the input crosses the threshold.

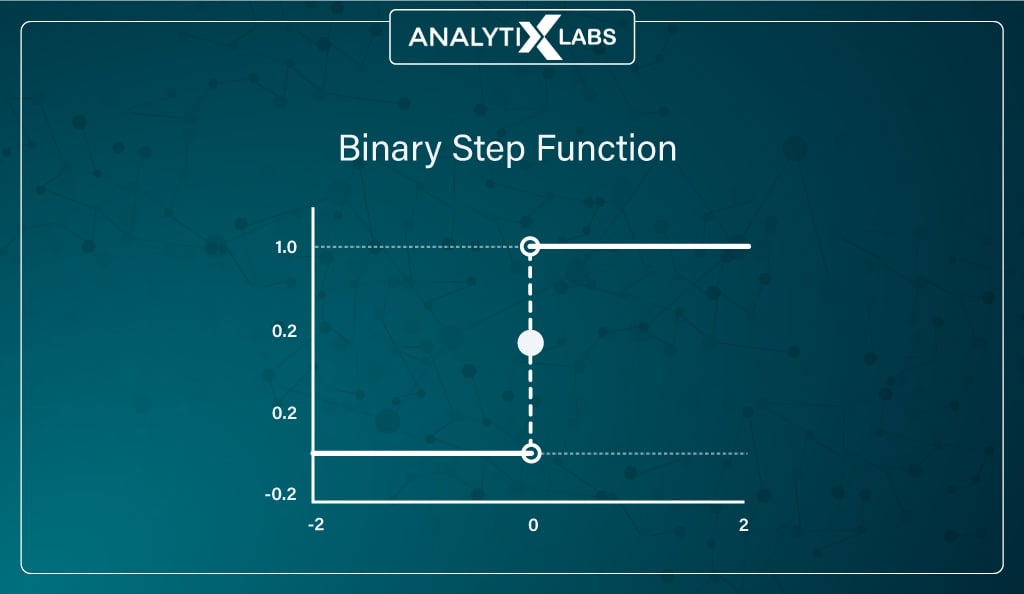
As you can imagine, such an activation function creates a binary classifier. The issue with using such a function is that it cannot return multiple outputs, i.e., it cannot work with multiclass classification output. Also, backpropagation cannot work because the gradient of the binary step function is zero, causing issues in the backpropagation process.

Types of Activation Function in Neural Network

A common question asked during AI-based interviews is, ‘Which all are activation functions?‘ The answer to that is that there are many types of activation functions.

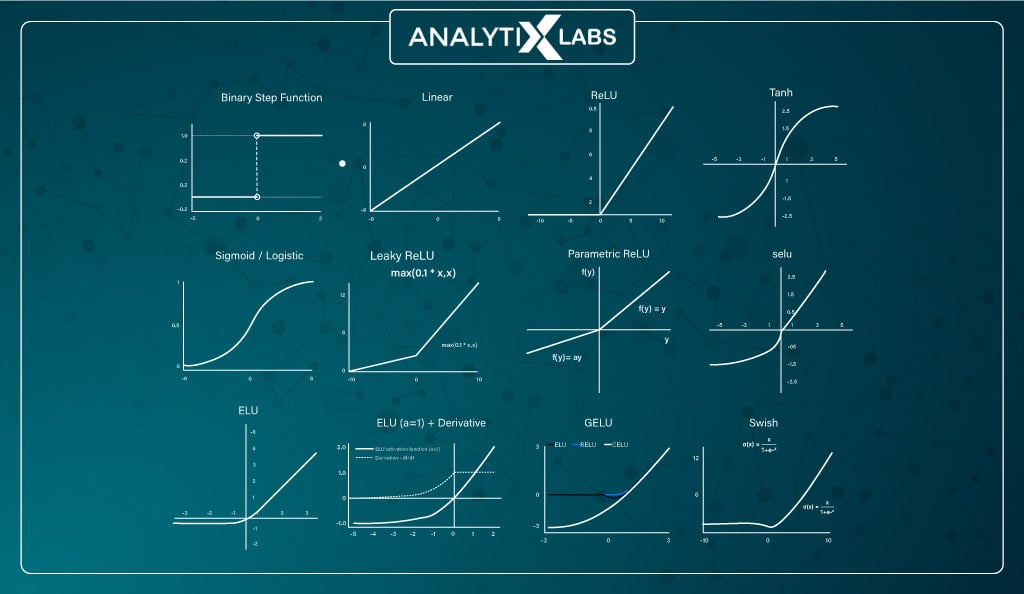
While we have already discussed Linear and Binary Step functions, this section will focus on the numerous non-linear activation functions.

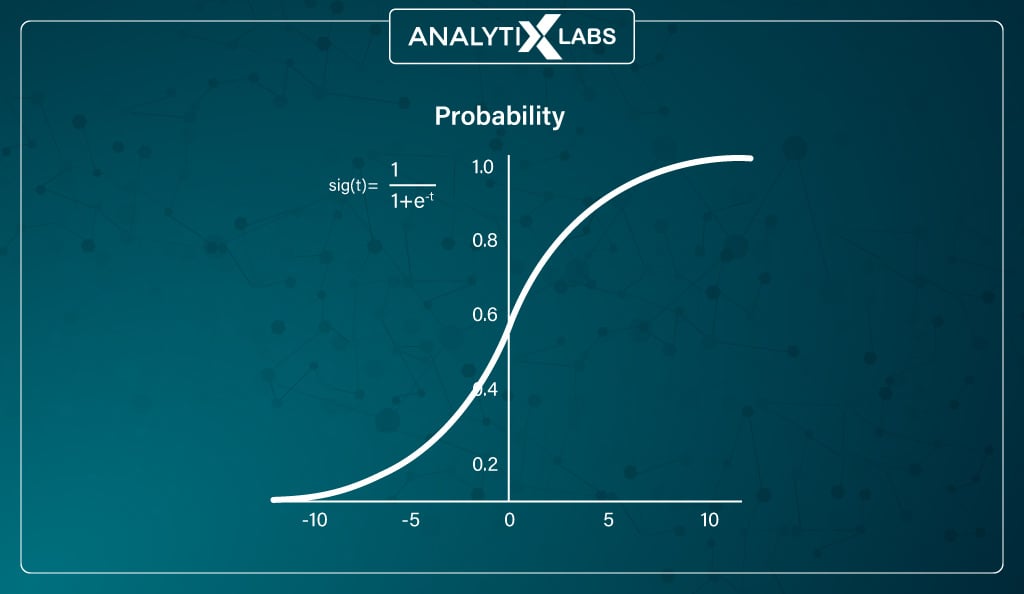
#1. Sigmoid (logistic) function

Mathematically represented as:

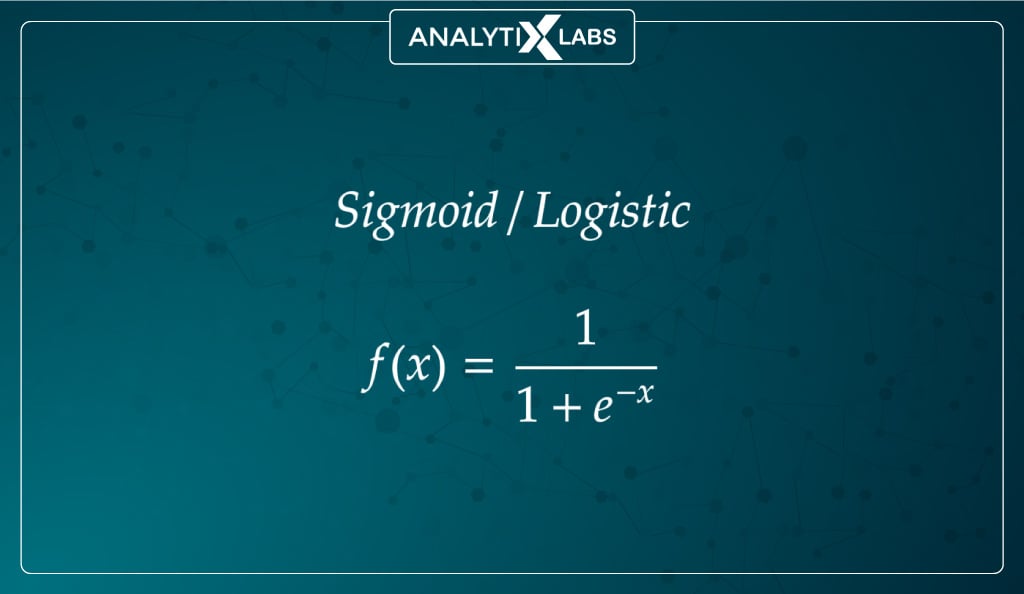
The sigmoid or logistic activation function is the most widely used. It can accept any real value and squishes the output values to be between 0 and 1, with larger input closer to 1 and smaller closer to 0.

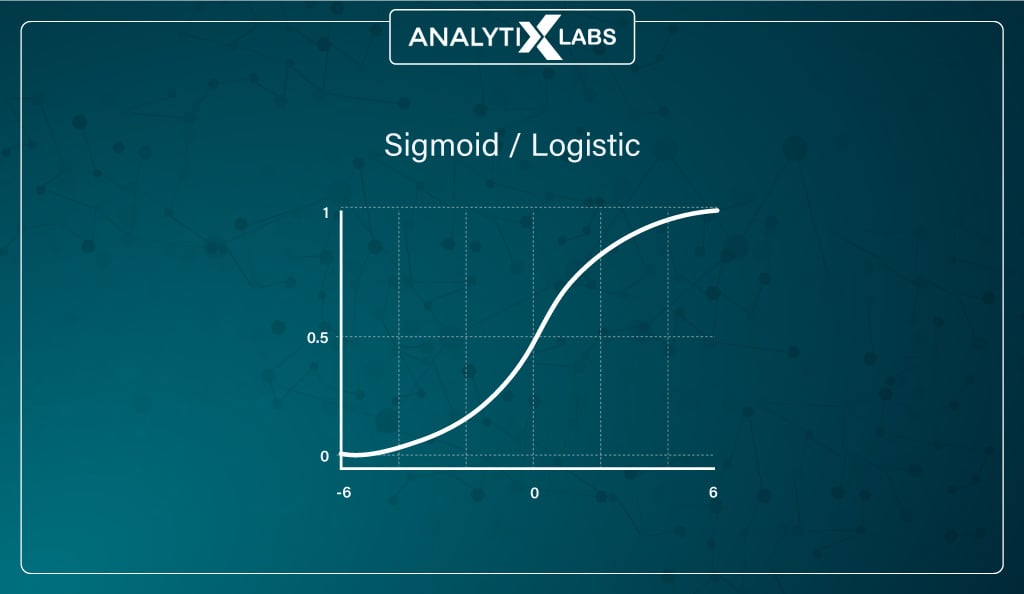
It’s typically used where the network needs to predict probabilities. It’s also useful as it provides a smooth gradient (represented by the S-shaped sigmoid function), ensuring values don’t jump in the output.

The derivative function of the sigmoid activation function is

f’(x) = sigmoid(x)  * (1-sigmoid(x))

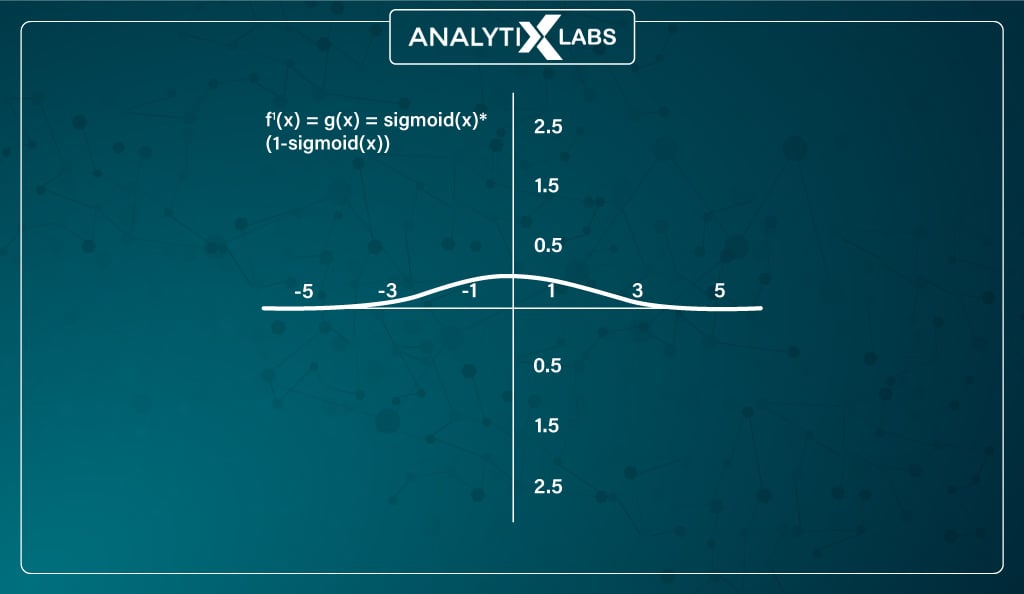
The function, while differentiable, suffers from a few issues. The gradient values of the sigmoid function in neural networks are significant between -3 and 3, making values outside this range have a small gradient.

This causes the vanishing gradient problem where the gradient value approaches zero, and the ability of the network to learn starts to suffer. Also – 

Training a network with a sigmoid activation function is difficult and unstable. This is because the output of such a function is not symmetric around zero, causing all neurons to have the same sign in the output.

Thus, the logistic activation function is typically used in the output layers, where the output is expected to return probabilities for a binary class classification problem.

#2. Tanh (hyperbolic tangent) function

Mathematically represented as –

While Tanh is similar to the sigmoid activation function because it has an S-shape. However, it is different because, unlike sigmoid, whose output is between 0 and 1, the output of tanh is between -1 and 1, with larger input being closer to 1 and smaller being closer to -1.

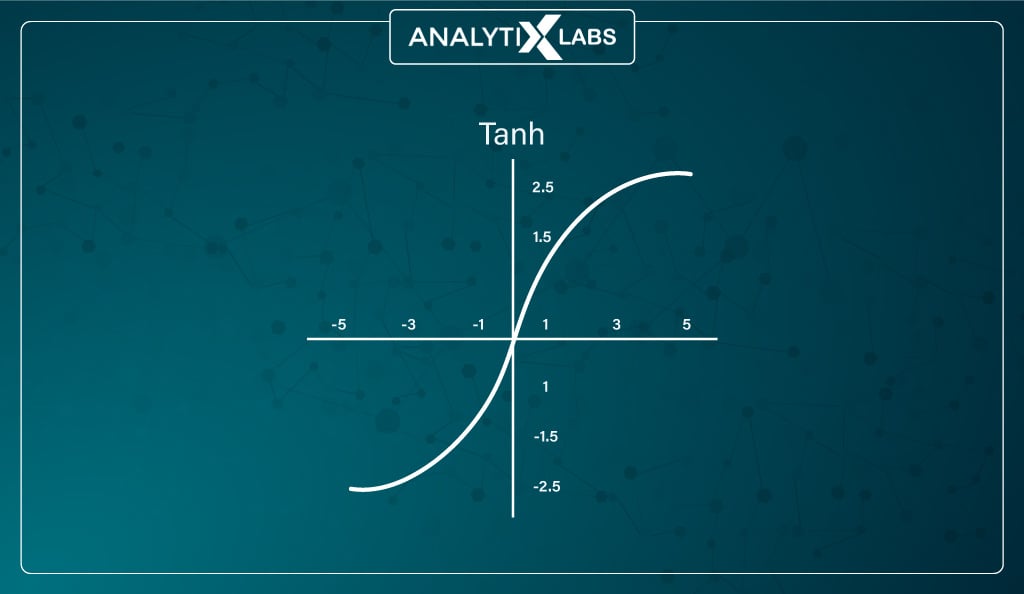
The advantage of such a function is that it can easily map output in terms of neutral, significantly positive, or significantly negative because it is zero-centered in its design.

Also, it is easy for the neural network to learn when using such a function because of its -1 to 1 range, as the mean of the hidden layer can come close to 0, helping the network to center the data.

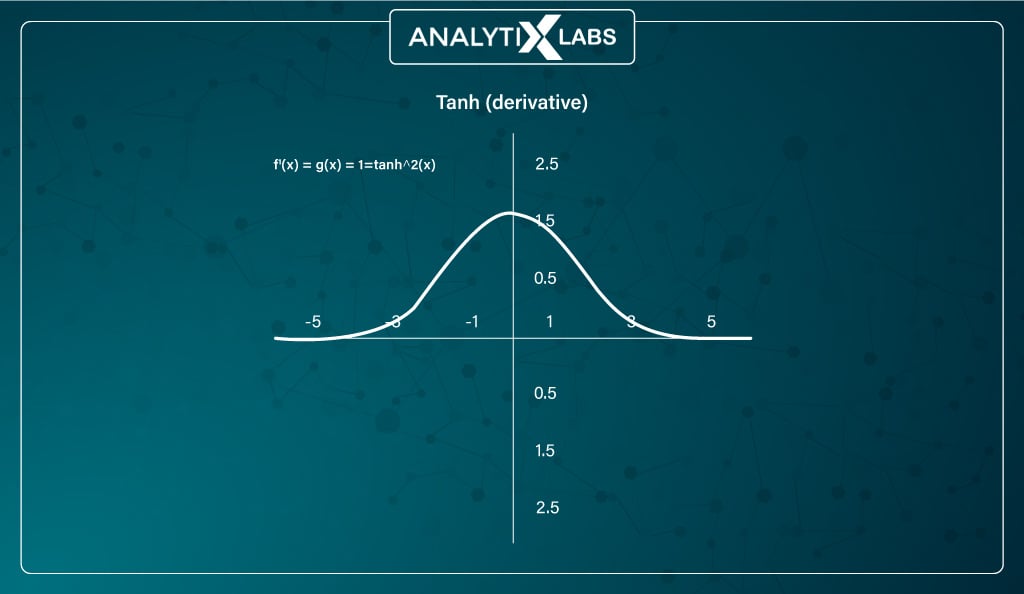
However, the function faces the same vanishing gradient problem as the sigmoid function, with a steeper gradient. However, tanh is still preferred over sigmoid mainly because it is zero-centered, which allows the gradient to move in both directions allowing tanh non-linearity to be preferred over sigmoids.  

#3. ReLU function

Mathematically represented as –

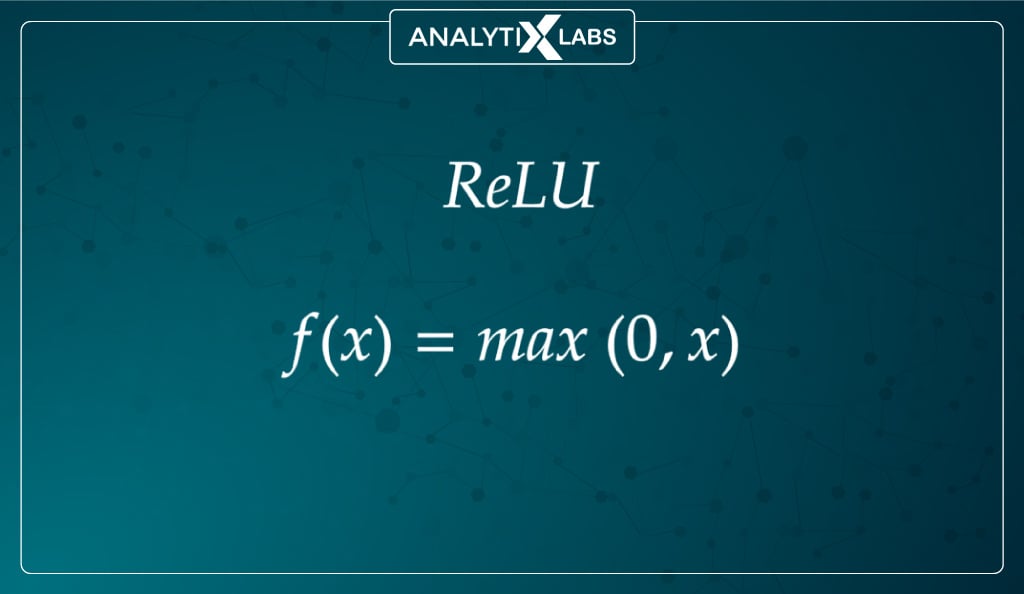
The ReLU function can easily be considered nearly a linear function, and in a way, it is a piecewise linear function with two linear pieces. However, because it has a derivative function, it’s considered a non-linear activation function and allows for backpropagation.

The function allows the network to be computationally efficient, keeping the neurons deactivated when the linear transformation’s output is less than 0. Another advantage is that its linear properties (for the output greater than 0) provide the impetus for the convergence of the gradient descent towards the global minima of the loss function.

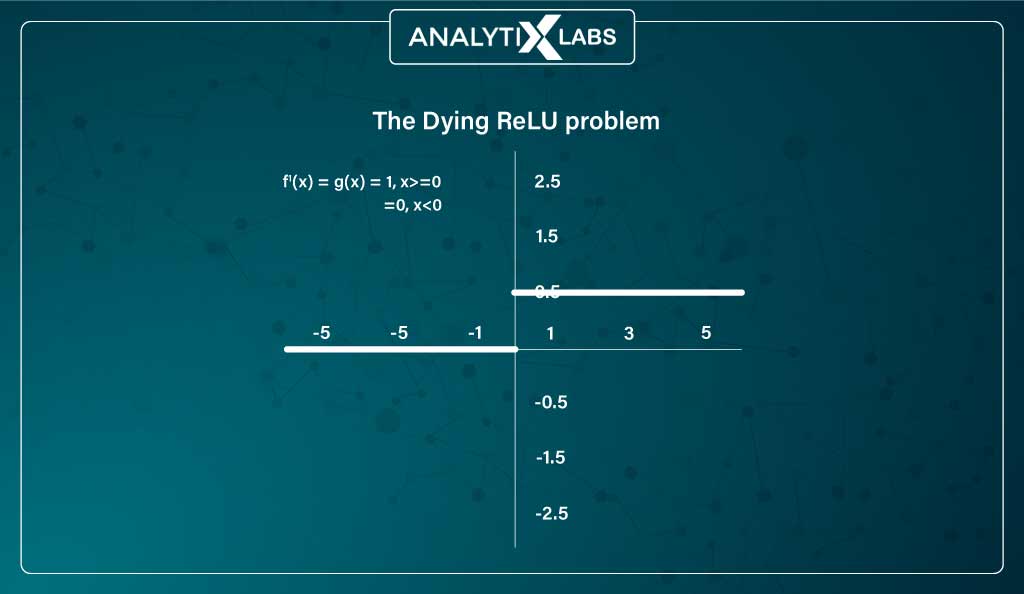
The issue with ReLU is a peculiar one known as the problem of dying ReLU where for the negative side, the gradient becomes zero, causing weights and biases not to get updated during backpropagation, hence creating ‘dead neurons’. This issue decreases the network’s ability to fit the data properly.

#4. Leaky ReLU function

Mathematically represented as –

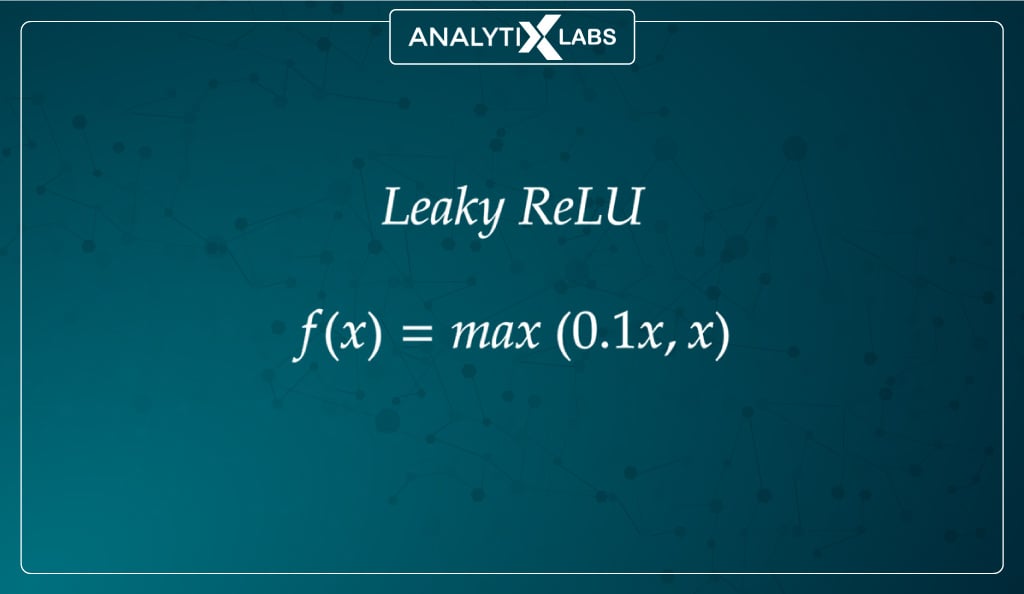
Given the advantages of ReLU, researchers have been working on the dying ReLU problem and have come up with an improved version known as Leaky ReLU.

Leaky ReLU returns a non-zero output rather than the negative values returning a zero output (as is the case with ReLU).

Therefore, rather than the previous horizontal line, there is a non-horizontal sloped line for the negative part, allowing backpropagation for negative input values, bypassing the ‘dead neuron’ problem.

However, some issues remain, such as that prediction will be inconsistent for negative input values and the gradient (while not zero) will be small, making the learning of parameters to be slow.

#5. PReLU (Parametric Rectified Linear Unit) function

Mathematically represented as –

Another variant of ReLU aimed at resolving the dying neurons problem is Parametric ReLU.

Here, the negative input values slope is provided through an argument α. During backpropagation, α is tuned, and its best value is learned. It is popularly used as an alternative to Leaky ReLU.

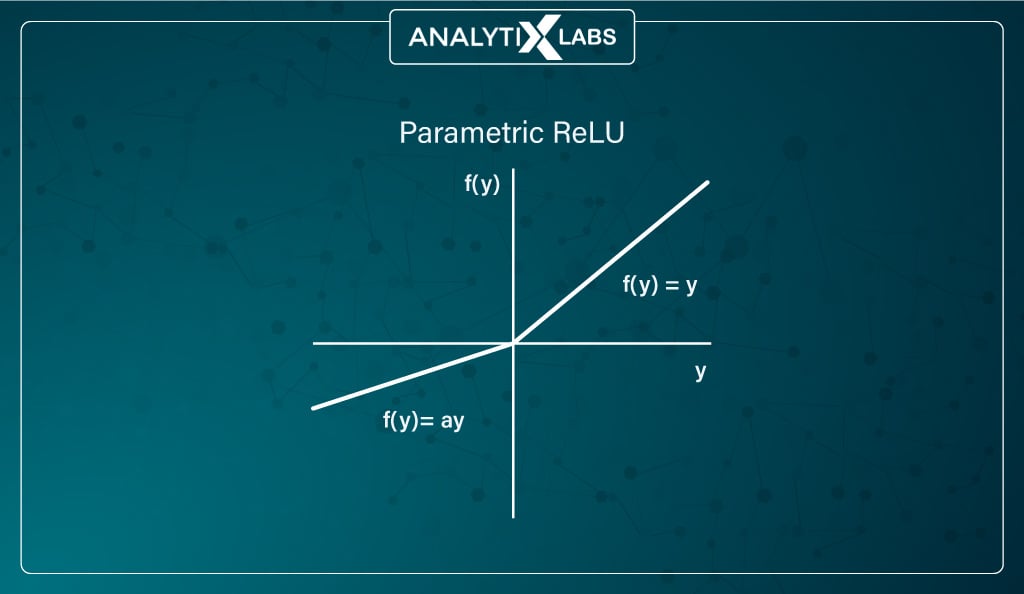
The unfortunate fact of parametric ReLU is that by allowing tuning the activation function itself, the issue of inconsistency appears as it performs differently for different problems. This is because the function’s behavior depends on the value of α, i.e., the slope parameter. 

#6. ELUs (Exponential Linear Units) function

Mathematically represented as –

ELU is yet another attempt at resolving the issue of ReLU. Here the slope for the negative part of the function is modified such that a log curve is used.

ELU doesn’t have a straight line like ReLU, Leaky ReLU, and parametric ReLU and becomes gradually smooth, unlike sharply smooth others.

ELU becomes gradually smooth until the output is the same as –α.

The introduction of a log curve resolves the problem of dead neurons and allows the network to judge better the direction in which the weights and biases need to be tuned.

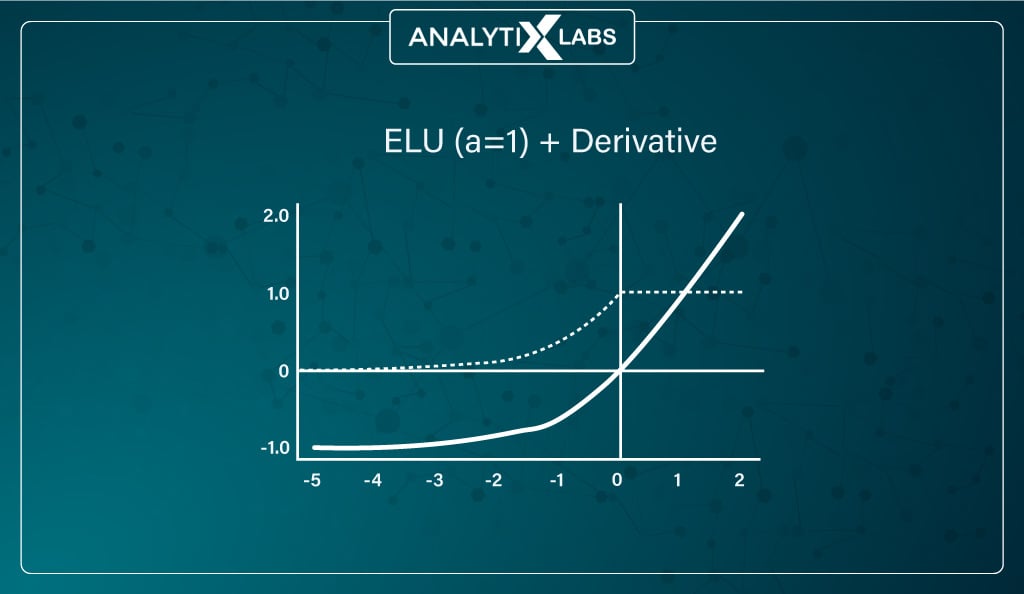
The log function stands as –

With all these innovations, there are still a few issues with ELU, such as the associated computational time because of the exponential operation, lack of learning for the slope parameter α, and exploding gradient problem (i.e., the accumulation of significant error gradients resulting in abnormally large updates to the parameters causing hindrance in the learning process).

#7. Softmax function

Mathematically represented as –

Softmax, also known as the soft argmax function or multiclass logistic regression function, is a non-linear function. It’s typically used for handling multiclass problems as it acts like a combination of multiple sigmoid functions.

Like the sigmoid function, it squeezes the output between 0 and 1 for each mutually exclusive class of the target variable. Like the sigmoid function, softmax is typically used in the output layer to get probabilities in the output.

#8. Swish function

Mathematically represented as –

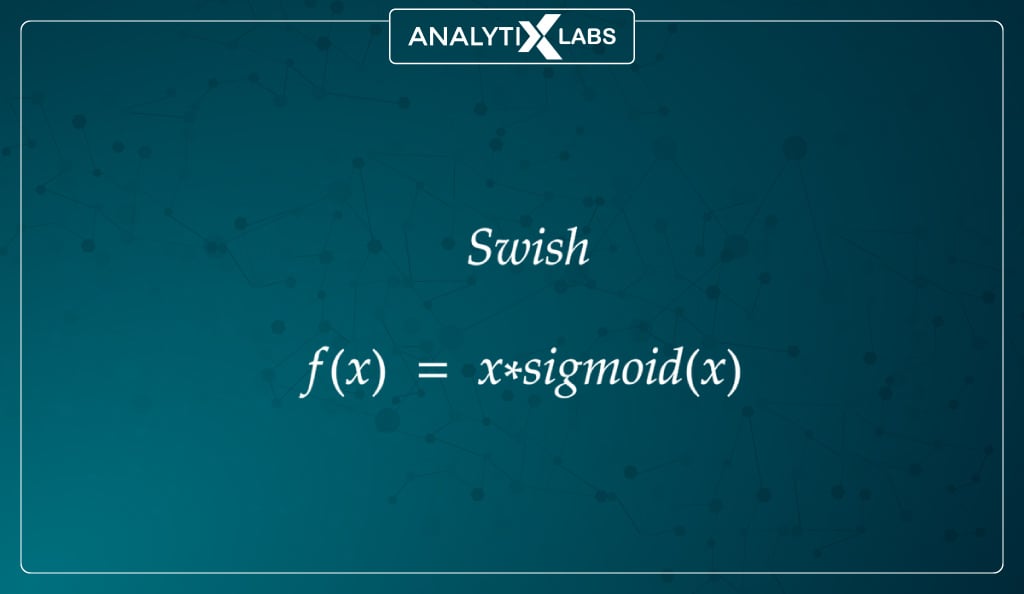
Developed by Google, this function often outperforms ReLU, and just like it, it is also applied to solve difficult problems like machine translation, image classification, etc.

The function is a combination of bounded and unbounded, as its unbounded above but bounded below. The Swish function doesn’t abruptly change direction (the way ReLU does near x = 0), gradually bends from 0 towards the negative values, and then moves upwards.

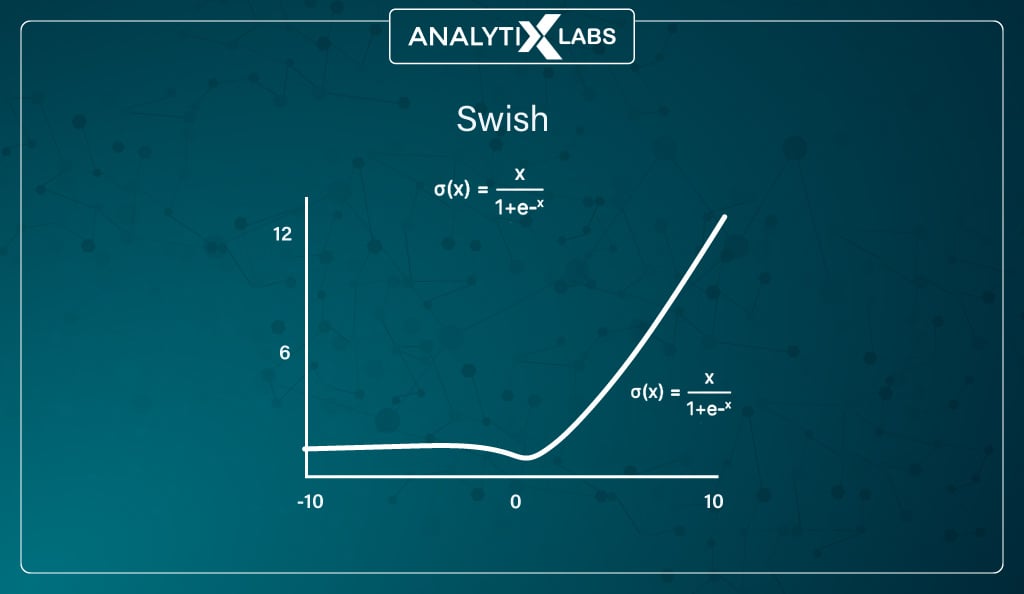
Because of this bend, unlike ReLU, which eliminated negative values that might be crucial to capture patterns in the data, the Swish function can retain the negative values and only zeros out the large negative values.

#9. GELU (Gaussian Error Linear Unit) function

Defined mathematically as –

This activation function combines RELU, Dropout, and Zoneout properties. Let’s quickly understand these properties. Dropout is a regularization mechanism that works by stochastically multiplying a few activations by zero.

ReLU, too, does this by deterministically multiplying the input by zero or one (based on whether the input value is positive or negative) rather than randomly.

Zoneout is another regularization mechanism commonly used in recurrent neural networks (RNN). It randomly forces a few hidden units to maintain their previous values by stochastically multiplying a few activations by 1.

These methods help the networks become computationally effective and add noise to train a pseudo-ensemble that improves generalization.

GELU combines all these properties so that the function randomly multiplies the input by 1 or 0 and gets the output from the activation function deterministically.

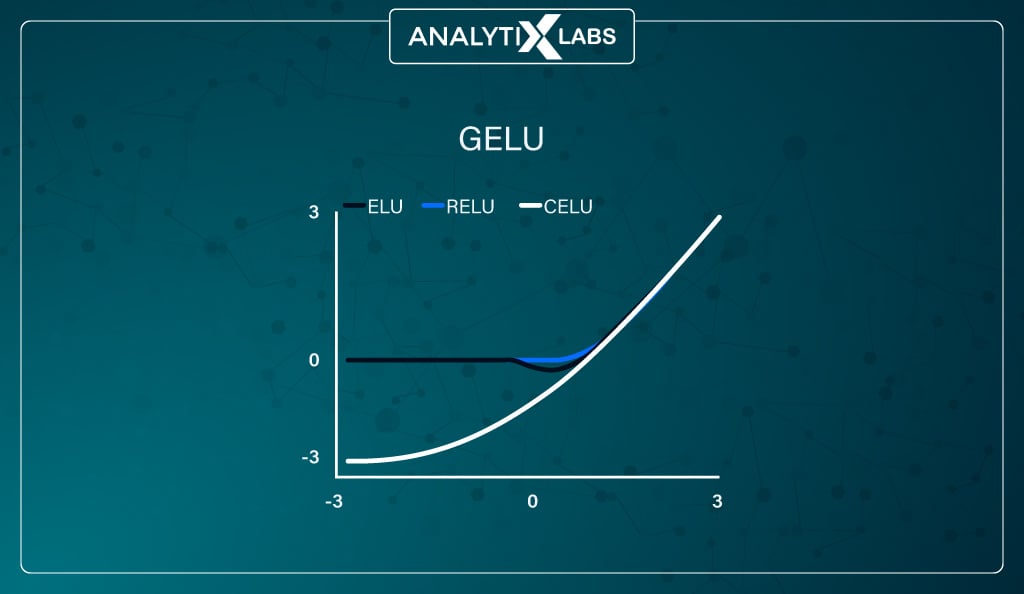
GELU is commonly used with NLP modes such as BERT, ALBERT, ROBERTa, etc. As it’s created by combining properties of RELU, Zoneout, and Dropout, its non-linearity is considered better than ReLU and ELU, especially for performing tasks related to NLP, Computer Vision, Speech Recognition, etc.

#10. SELU (Scaled Exponential Linear Unit) Function

Mathematically represented as –

The values of α and λ are predefined for the function to work.

SELU performs internal normalization by preserving the mean and variance of each layer from the previous layers making it a self-normalizing network. This preservation is achieved by adjusting the mean and variance.

Both negative and positive values are used to shift the mean. Such a mechanism is impossible for activations functions like ReLU as it does produce negative values.

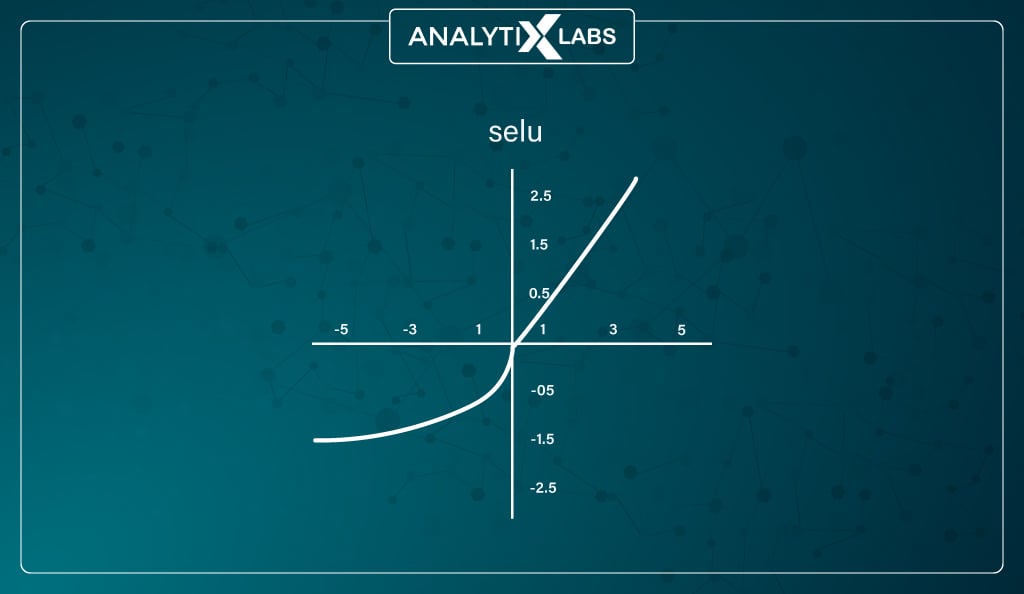
The variable in SELU is adjusted using gradients. As external normalization is slower than internal normalization, SELU has the edge over other networks as it converges quickly. The limitations of this function are yet to be explored as it’s a relatively new function, and researchers need to analyze its performance on networks like CNN and RNN.

Rules to Choose the Right Function

As you can see, there are many activation functions to choose from. If you feel confused regarding which one to use, then you can remember a few basic rules. These include-

• Avoid using ReLU in the output layer and Sigmoid, Tanh, and Softmax in hidden layers
• Only use the Swish activation function when network depth > 40
• In the output layer, use linear activation for regression problems, sigmoid for binary classification, and softmax for multiclass classification problems
• Choose the activation functions in the hidden layers based on the network architecture; for example, ReLU is associated with CNN, while Sigmoid or Tanh is with RNN
• If confused, use ReLU in hidden layers and linear / sigmoid /softmax in the output layer for regression, classification, and multiclass classification problems, respectively

Conclusion

The activation function plays an important role in neural networks and can be considered the backbone of Artificial Intelligence. Due to the activation function, non-linearity can be introduced to the network, which allows it to solve complex problems.

While many different activation functions can be applied in the hidden layers, the most common one being ReLU, all the neurons in the hidden layer typically have the same activation function. The activation function in hidden layers needs to be differentiable so that the backpropagation can learn the correct parameters of the network.

Regarding the output layer, the activation function here needs to be per the expected range of output values; typically, for a binary output, the sigmoid function is used, while for numerical output, linear activation or sometimes ReLU is considered.

The field of activation function is constantly evolving, and you must keep an eye out for the latest development in the field, as activation function can considerably enhance the capability of a network.

FAQs

• Why is ReLU used in CNN?

CNN is generally used when dealing with images where much data needs to be processed. ReLU, as it is simple to calculate, and derivatives of 1 or 0 allow for preventing the exponential growth in computation required for CNN. Therefore, if using ReLU and a CNN network scales in size, the cost of adding additional ReLUs increases linearly.

• What are the three activation functions?

While there are many kinds of activation functions in neural networks, the three main types of activation functions are linear, non-linear, and binary step.

• What does ReLU stands for?

ReLU stands for Rectified Linear Unit.

• What is activation with example?

A simple example of an activation function can be a sigmoid function where x1 and x2 are inputs, and w1 and w2 are their respective weights, with b0 being the bias. A sigmoid function in the node will act like a logistic regression model, as the output will be between 0 and 1.

• What is ReLU in deep learning?

In deep learning, ReLU refers to an activation function typically used in the hidden layers. It’s unique as it acts as a linear function for values greater than zero but reruns zero for negative values, making it a non-linear function.