What Is Regularisation and Its Importance in Machine Learning?

If you have been working on business case problems using Machine or Deep Learning techniques or participating in some of the data science hackathons, you would certainly have faced the situation where your training accuracy is very high, and the testing accuracy is not.

The reason this happens is because of the inevitable trade-off between bias and variance error. If you want to make functional machine learning or deep learning models, you can not escape this trade-off. Therefore, to understand what regularization is in machine learning and why it is needed, it is crucial to understand the concept of the bias-variance trade-off and its impact on the model.

In this article, we shall explore and understand what regularization in machine learning is, how regularization works, regularization techniques in machine learning, the regularization parameter in machine learning, and some of the most frequently asked questions.

If you are new to Machine Learning, then I would encourage you to first understand the Basics of Linear Regression and Logistics Regression before venturing into the world of Regularization.

Related: What Are the Important Topics in Machine Learning?

AnalytixLabs, India’s top-ranked AI & Data Science Institute, is led by a team of IIM, IIT, ISB, and McKinsey alumni. The institute provides a wide range of data analytics courses inclusive of detailed project work, which helps an individual fit for the professional roles in AI, Data Science, and Data Engineering. With its decade of experience in providing meticulous, practical, and tailored learning, AnalytixLabs has proficiency in making aspirants “industry-ready” professionals.

The Problem of Overfitting

So, before diving into regularization, let’s take a step back to understand what bias-variance is and its impact.

Bias is the deviation between the values predicted by the model and the actual values whereas, variance is the difference between the predictions when the model fits different datasets.

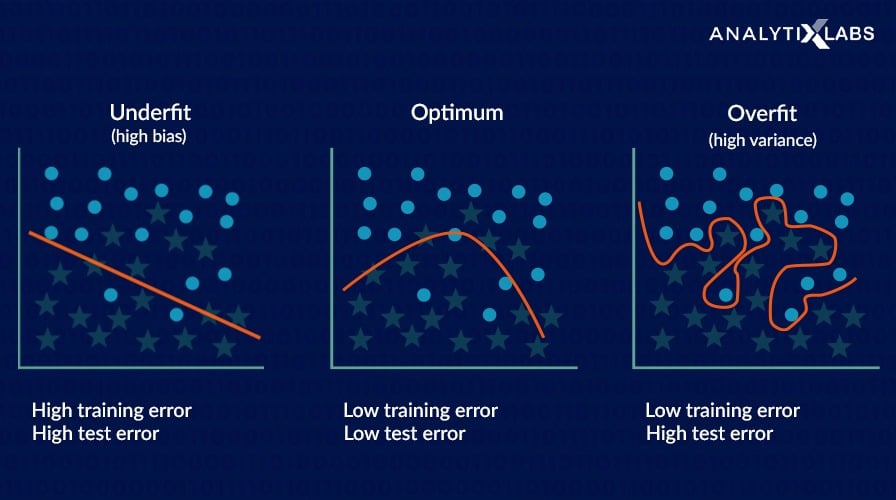
In the above panel, the rightmost graph shows that the model can perfectly differentiate between the green and purple points. This is on the training data. In this case, the bias is low. In fact, it can be said to be zero since there is no difference between the predicted and the actual values. This model will give accurate predictions.

However, it will not give this result consistently. Why? Because it may predict well on the train data, but the unseen (or the test) data does not contain the same data points as that of the train data. Therefore, it will fail to produce the same results consistently and hence can not generalize on the other data.

When a model performs well on the training data and does not perform well on the testing data, then the model is said to have high generalization error. In other words, in such a scenario, the model has low bias and high variance and is too complex. This is called overfitting.

Overfitting means that the model is a good fit on the train data compared to the data, as illustrated in the graph above. That’s the reason whenever you build a model; it is said to maintain the bias-variance trade-off. Overfitting is also a result of the model being too complex.

So, how do we prevent this overfitting? How to ensure that the model predicts well both on the training and the testing data? One way to prevent overfitting is Regularization, which leads us to what regularization is in machine learning.

What Is Regularization in Machine Learning?

There is a principle called Occam’s Razor, which states: “When faced with two equally good hypotheses, always choose the simpler.”

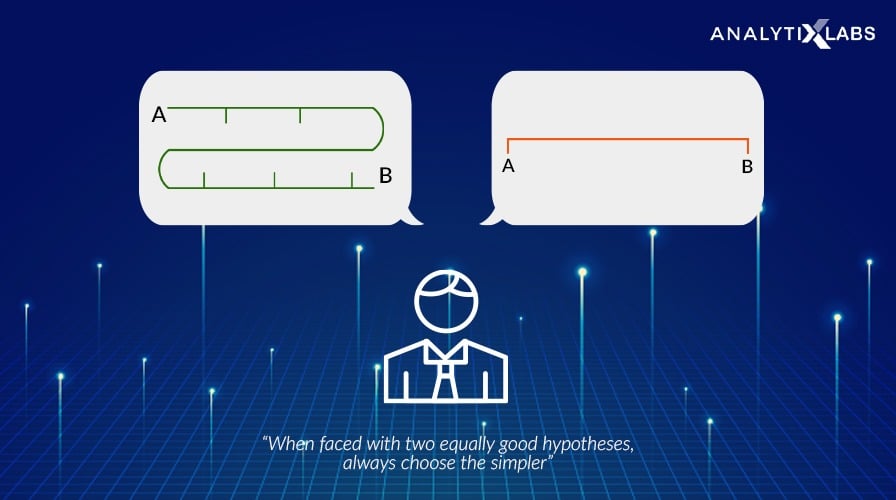
Regularization is an application of Occam’s Razor. It is one of the key concepts in Machine learning as it helps choose a simple model rather than a complex one.

As seen above, we want our model to perform well both on the train and the new unseen data, meaning the model must have the ability to be generalized. Generalization error is “ a measure of how accurately an algorithm can predict outcome values for previously unseen data.” 

Regularization refers to the modifications that can be made to a learning algorithm that helps to reduce this generalization error and not the training error. It reduces by ignoring the less important features. It also helps prevent overfitting, making the model more robust and decreasing the complexity of a model.

The regularization techniques in machine learning are:

• Lasso regression: having the L1 norm
• Ridge regression: with the L2 norm
• Elastic net regression: It is a combination of Ridge and Lasso regression.

We will see how the regularization works and each of these regularization techniques in machine learning below in-depth.

How Does Regularization Work?

Regularization works by shrinking the beta coefficients of a linear regression model. To understand why we need to shrink the coefficients, let us see the below example:

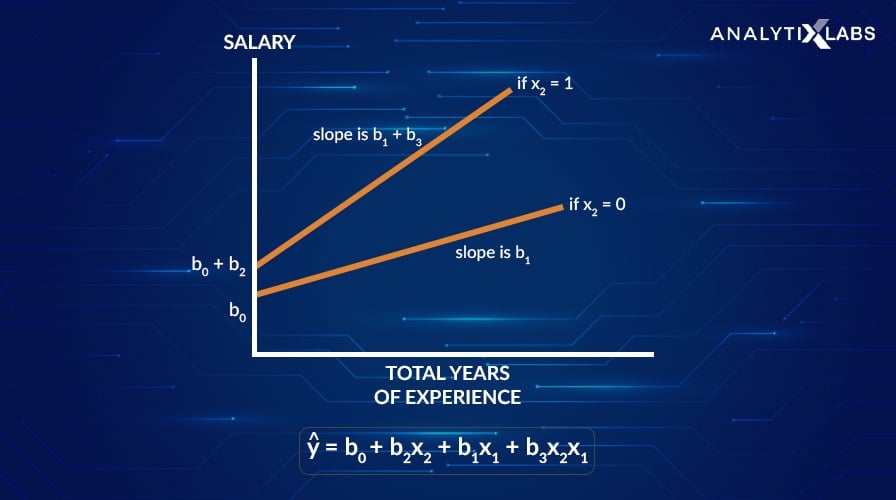
In the above graph, the two lines represent the relationship between total years of experience and salary, where salary is the target variable. These are slopes indicating the change in salary per unit change in total years of experience. As the slope b1 + b3 decreases to slope b1, we see that the salary is less sensitive to the total years of experience.

By decreasing the slope, the target variable (salary) became less sensitive to the change in the independent X variables, which increases the bias into the model. Remember, bias is the difference between the predicted and the actual values.

With the increase in bias to the model, the variance (which is the difference between the predictions when the model fits different datasets.) decreases. And, by decreasing the variance, the overfitting gets reduced.

The models having the higher variance leads to overfitting, and we saw above, we will shrink or reduce the beta coefficients to overcome the overfitting. The beta coefficients or the weights of the features converge towards zero, which is known as shrinkage.

Now, to do this, we penalize the model that has higher variance. So, Regularization adds a penalty term to the loss function of the linear regression model such that the model with higher variance gets a larger penalty.

What Is the Regularization Parameter?

For linear regression, the regularization has two terms in the loss function:

1. The Ordinary Least Squares (OLS) function, and
2. The penalty term

It becomes :

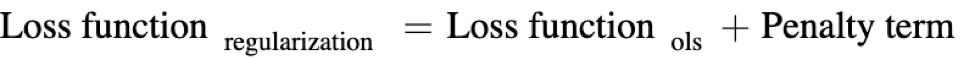
The goal of the linear regression model is to minimize the loss function. Now for Regularization, the goal becomes to minimize the following cost function:

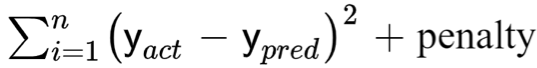
Where, the penalty term comprises the regularization parameter and the weights associated with the variables. Hence, the penalty term is:

The regularization parameter in machine learning is λ :

• It imposes a higher penalty on the variable having higher values, and hence, it controls the strength of the penalty term.
• This tuning parameter controls the bias-variance trade-off.
• λ can take values 0 to infinity
• If λ = 0, then means there is no difference between a model with and without regularization.

We shall see the L-p norms in the following section while discussing the various regularization techniques.

Regularization Techniques in Machine Learning

Each of the following techniques uses different regularization norms (L-p) based on the mathematical methodology that creates different kinds of regularization. These methodologies have different effects on the beta coefficients of the features. The regularization techniques in machine learning as follows:

a. Ridge Regression

The Ridge regression technique is used to analyze the model where the variables may be having multicollinearity. It reduces the insignificant independent variables though it does not remove them completely. This type of regularization uses the L2 norm for regularization.

• It uses the L2-norm as the penalty.
• L2 penalty is the square of the magnitudes of beta coefficients.
• It is also known as L2-regularization.
• L2 shrinks the coefficients, however never make them to zero.
• The output of L2 regularization is non-sparse.

The cost function of the Ridge regression becomes:

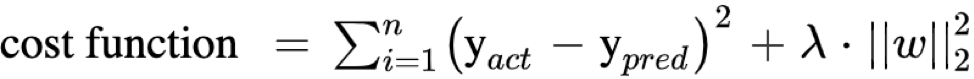
b. Lasso Regression

Least Absolute Shrinkage and Selection Operator (or LASSO) Regression penalizes the coefficients to the extent that it becomes zero. It eliminates the insignificant independent variables. This regularization technique uses the L1 norm for regularization.

• It adds L1-norm as the penalty.
• L1 is the absolute value of the beta coefficients.
• It is also known as the L-1 regularization.
• The output of L1 regularization is sparse.

It is useful when there are many variables, as this technique can be used as a feature selection method by itself. The cost function for the LASSO regression is:

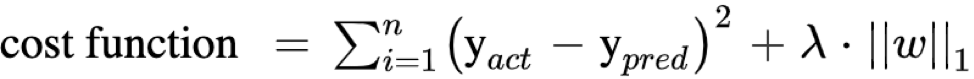
c. Elastic Net Regression

The Elastic Net Regression technique is a combination of the Ridge and Lasso regression technique. It is the linear combination of penalties for both the L1-norm and L2-norm regularization.

The model using elastic net regression allows the learning of the sparse model where some of the points are zero, similar to Lasso regularization, and yet maintains the Ridge regression properties. Therefore, the model is trained on both the L1 and L2 norms.

The cost function of Elastic Net Regression is:

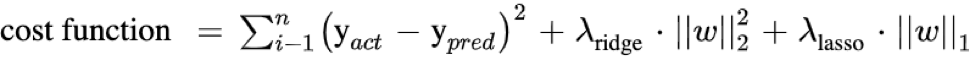
The regularization parameters for the implementation of Elastic Net Regression are:

• λ ,and
• L1 ratio

where, λ = λ(Ridge) + λ(Lasso) and is written as:

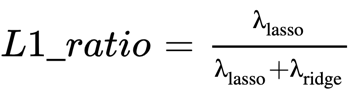
The formula for L1_ratio for all the methods becomes:

	Regularization Technique	Penalty
L1_ratio = 0	Ridge Regression	L-2
L1_ratio = 1	Lasso Regression	L-1
0< L1_ratio <1	Elastic Net Regression	Combination of L-1 and L-2

In Python, the strength of the penalty is controlled by the argument called alpha. If:

• alpha = 0, then will become Ridge, and
• alpha = 1, then it becomes Lasso.

The Elastic Net Regression happens in two stages:

• the first stage is Ridge Regression, and
• then the second stage is the LASSO Regression.

In each stage, the betas get reduced or shrunken, resulting in an increased bias in the model. An increase in bias means a lot of deviation between the predicted values and the actual values and therefore makes more predictions. Hence, we rescale the coefficients of Elastic Net Regularization by multiplying the estimated coefficients by (1+λridge) to improve the prediction performance and decrease the bias.

When to Use Which Regularization Technique?

The regularization in machine learning is used in following scenarios:

• Ridge regression is used when it is important to consider all the independent variables in the model or when many interactions are present. That is where collinearity or codependency is present amongst the variables.
• Lasso regression is applied when there are many predictors available and would want the model to make feature selection as well for us.
• When many variables are present, and we can’t determine whether to use Ridge or Lasso regression, then the Elastic-Net regression is your safe bet.

Related: How to Choose The Best Algorithm for Your Applied AI & ML Solution

Summary

Based on Occam’s Razor, Regularization is one of the key concepts in Machine learning. It helps prevent the problem of overfitting, makes the model more robust, and decreases the complexity of a model.

In summary, regularization chooses a model (making Occam’s Razor applicable) with smaller weights of the features (or shrunken beta coefficients) that have less generalization error. In addition, it penalizes the model having higher variance by adding a penalty term to the loss function to prevent the larger values from being weighed too heavily.

The regularization techniques are Lasso Regression, Ridge Regression, and Elastic Net Regression. Regularization can be used for feature reduction.

Data Science Career Potential

The most sought-after and precious skill in the job market is that of data science. The U.S Bureau of Labor Statistics has reported that in the next five years, by 2026, the demand for data science skills will increase employment by almost 28%.

It is one field that will certainly only grow. The demand for these skills will only continue to rise, and there is absolutely no way to slow that down. However, data science is surely a lucrative path, and as there are no free lunches, this path comes with its cost. The cost of being a data scientist is that you would need to upgrade your skills from being a generalist to being a specialist.  

It would be an understatement to say that the data is growing at the speed of light. By 2025, it is estimated that the data will grow to 175 zettabytes! With the humongous amount of data that we are already exposed to and which is coming our way, the skilled people to drive meaningful insights and use them for our benefit will survive the game. The data and demand for people with data science skills are here to stay, at least for the next few decades. It’s up to us how much we want to leverage out of this tsunami of information!

Related: Why Data Science Is Important And Why Do We Need It?

FAQs – Frequently Asked Questions

Q1. What are L1 and L2 regularization?

L1 and L2 are the norms of regularization. These are the types of regularization that help in reducing the overfitting problem by reducing the less important features. It is done by shrinking the beta coefficients of the linear regression model. The differences between L1 and L2 norms are as follows:

L1 regularization	L2 regularization
L1 is equal to the absolute value of the beta coefficients.	L2 is equal to the squares of magnitudes of beta coefficients.
It is used in Lasso regression.	It is used in Ridge regression.
To prevent overfitting, L1 estimates the median of the data.	L2 estimates the mean of the data to avoid overfitting.
L1 has built-in feature selection.	L2 is not used for feature selection.
L1 returns sparse outputs.	L2 results in non-sparse outputs.
It is computationally inefficient on the non-sparse cases.	It is computationally efficient since it has analytical solutions.

Q2. What is L1 and L2 Penalty?

• The L1 penalty is the absolute of the weights which are added to the loss function and are used in Lasso regression, whereas
• L2 penalty is the square of the weights. This penalty term is added to the loss function, which is used in Ridge regression.

Q3. What is an advantage of L1 regularization over L2 regularization?

L1 regularization shrinks the beta coefficients or the weights of the features in the model to zero and hence, is useful for eliminating the unimportant features. On the other hand, L2 regularization shrinks the weights evenly and is applicable when multicollinearity is present in the data. The advantage of L1 regularization over L2 is that L1 can be used for feature selection.

Q4. Is regularization helpful for logistic regression?

Yes, regularization is helpful for logistic regression. As the logistic regression is applied for classification problems, wherein the case of binary classification predicts whether it belongs to class 1 or class 0, therefore the loss function changes to:

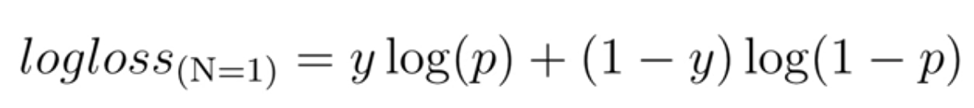
To understand in detail how the loss function for Logistic Regression works and gets updated post the regularization, refer to this blog here.

Q5. What is overfitting?

When the difference between the train error and test error is significant then the model is overfitting. For more detail understand please go through the complete post.

Q6. What is a bias-variance trade-off?

Bias measures how much deviation is between the actual and predicted values.Variance measures how much the prediction fluctuates for different datasets. Bias-Variance trade-off is the balance between the error due to the bias and the variance.

Hope this blog helps you understand the regularization in Machine Learning and its importance in dealing with the problem of overfitting. For a practical and in-depth understanding of many more such important machine learning concepts, check out our Python Machine Learning Course!

You may also like to read: 

1. Top 75 Natural Language Processing (NLP) Interview Questions

2. Top 60 Artificial Intelligence Interview Questions and Answers

3. Top 45 Machine Learning Interview Questions and Answers

4. Top 50 Data Science Interview Questions & Answers