What are Lasso and Ridge Techniques?

Regression analysis is a fundamental technique in data science. It allows professionals to predict continuous values based on given input features. As the importance of data-driven decision-making grows across various industries, understanding various regression analysis techniques has become vital for data engineers and data science professionals. Lasso and Ridge Regression are the two most popular regularization techniques used in Regression analysis for better model performance and feature selection.

This article will discuss their concepts and applications, underline their differences, and provide practical examples of implementing these techniques in Python. 

Let’s start by addressing the core concept of regression.

What is Regression?

Regression is a type of statistical technique used in data science to analyze the relationship between variables.

It typically involves finding the line of best fit for a given set of data points, estimating how much variation can be explained by that model, and predicting the value of one variable (known as the dependent variable) based on the values of others (known as independent variables).

Regression analysis is essential for understanding relationships among variables and making predictions.

A  key concept in Regression is fitting a line to a set of data points .

This process involves finding parameters such as intercept and slope, which describe how well the line fits the data. Different regression techniques, including Lasso and Ridge Regression, are used to optimize this fit. 

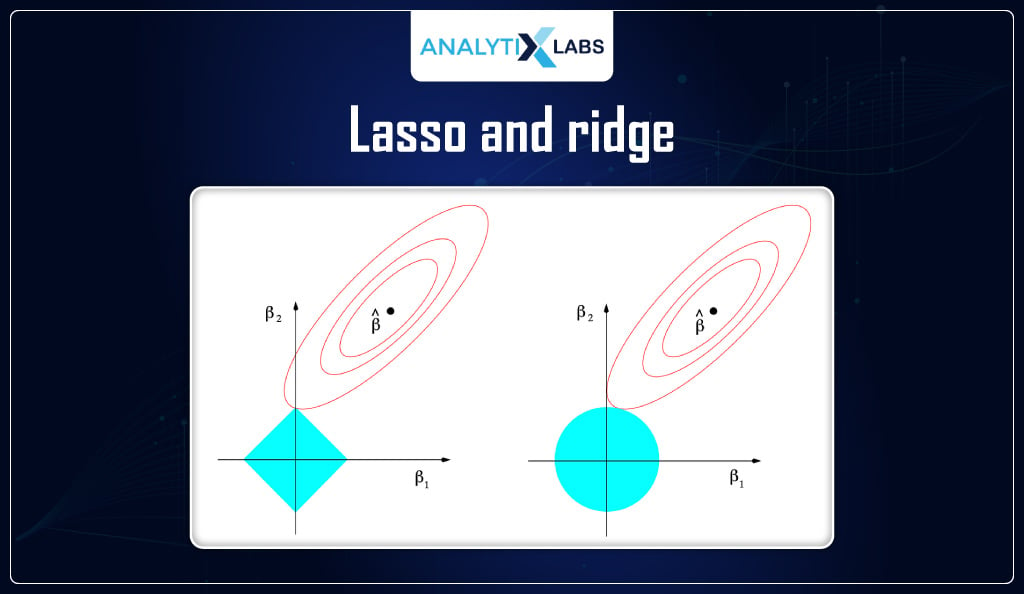
• Lasso Regression is a form of regularization that seeks to minimize the magnitude of coefficients so that more relevant variables are included in the model.
  
• Ridge Regression works by introducing an additional term that penalizes large coefficient values. Both techniques help to reduce overfitting and improve prediction accuracy.

Why Regression is Important for Data Science?

Regression is an important tool for data science because it

1.  Lets you identify relationships between variables
2. Make predictions based on those relationships
3. Assess how well a given model fits our data

Regression can be used for various applications, such as predicting stock prices or sales figures, assessing consumer behavior patterns, or determining medical outcomes based on patient characteristics.

By finding the best-fit line between two sets of variables, you can dig deeper into their relationships and use them to make better decisions. 

Whether it is predicting market trends or finding patterns in customer data, Regression is an invaluable tool for data science that helps us gain deeper insight into complex relationships.

With the right technique and enough data, this powerful tool can unlock all kinds of insights that would otherwise remain hidden. As a result, it makes  Regression an essential part of any data scientist’s toolbox .

Let us look at the two most popular regression techniques – Ridge and Lasso regression.

Ridge Regression

Ridge Regression, also known as L2 regularization, is an extension to linear Regression that introduces a regularization term to reduce model complexity and help prevent overfitting.

In simple terms, Ridge Regression helps minimize the sum of the squared residuals and the parameters’ squared values scaled by a factor (lambda or α). This regularization term, λ, controls the strength of the constraint on the coefficients and acts as a tuning parameter.

L2 Regularization or Ridge Regression seeks to minimize the following:

The Ridge Regression can help shrink the coefficients of less significant features close to zero but not exactly zero. By doing so, it reduces the model’s complexity while still preserving its interpretability.

An Example of Ridge Regression

Let’s consider a data set with three explanatory variables: A, B, and C.

You can use Ridge Regression to determine how each of these variables affects the response variable Y. Ridge Regression will add a regularization term (λ) to the equation to reduce the overall complexity of the model.

The modified equation is as follows:

By adding this regularization term, you can ensure that none of your features greatly impact your response variable. This helps avoid overfitting and keep interpretability while still getting useful results from your model.

Ridge Regression offers other benefits, such as improved generalization accuracy and reduced variance.

Ridge Regression is an important tool in statistical analysis, adding a regularization term to the linear Regression equation.

It helps reduce model complexity while preserving interpretability and preventing overfitting. It is a useful technique for many data science problems.

Lasso Regression

Lasso (Least Absolute Shrinkage and Selection Operator) Regression is another regularization technique that prevents overfitting in linear Regression models.

Like Ridge Regression, Lasso Regression adds a regularization term to the linear Regression objective function.

The difference lies in the loss function used – Lasso Regression uses L1 regularization, which aims to minimize the sum of the absolute values of coefficients multiplied by penalty factor λ.

L1 Regularization or Lasso Regression seeks to minimize the following:

Unlike Ridge Regression, Lasso Regression can force coefficients of less significant features to be exactly zero.

As a result, Lasso Regression performs both regularization and feature selection simultaneously.

An Example of Lasso Regression

Consider a dataset with two predictor variables, x1 and x2, and the response variable y. Suppose you are fitting a linear Regression model to predict y using the data points from the above features. You add an L1 Regularization or Lasso penalty to the objective function (as mentioned above):

Let’s say that after optimization, the Regression equation becomes:

`y = 0.4x1 - 0.3x2 - 0.5`

This equation clearly shows that the coefficient for x2 is zero. Hence, it has been eliminated from the model due to the L1 Regularization. This allows you to reduce your model’s complexity and prevents overfitting.

Therefore, Lasso Regression lets you select only the important features in a given dataset while reducing the complexity of the model.

It can be used as an alternative to feature selection methods such as stepwise Regression but with additional benefits like regularization, which can help prevent overfitting.

Additionally, since it forces some coefficients to be exactly zero, it is useful for identifying unimportant features that can be dropped from the model.

Difference Between Ridge and Lasso Regression

Ridge and Lasso Regression are two important regularization techniques used to address the issue of multicollinearity in linear Regression. Although they both use shrinkage, there are the following points of difference between Lasso and Ridge Regression.

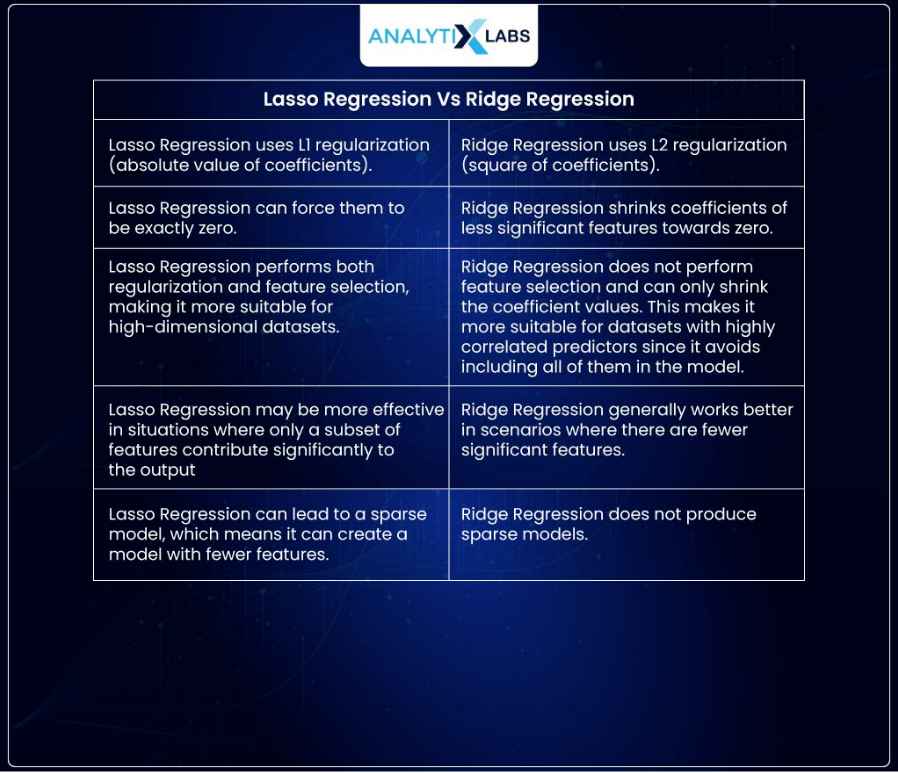
Looking at these points of difference between Lasso and Ridge Regression, we can conclude that Lasso Regression is better suited for feature selection.

In contrast, Ridge Regression is better at reducing the complexity of the model and avoiding overfitting. Depending on your data and objectives, one or both techniques may be necessary to obtain accurate predictions.

What is Regularization?

Regularization is a technique used in machine learning to penalize complex models to protect them from overfitting.

By doing this, regularization helps to prevent models from over-interpreting the noise and randomness found in data sets.

The two main types of regularization are

1. Lasso Regularization
2. Ridge Regularization

Lasso Regularization

Lasso Regression for Regularization, or L1 regularization, adds a penalty equal to the absolute value of the weights associated with each feature variable.

Lasso regularization encourages sparsity by forcing some coefficients to reduce their values until they eventually become zero while others remain unaffected or shrink less dramatically.

It is useful for selecting important features because it reduces the complexity of models by removing irrelevant variables that do not contribute to the overall prediction.

Ridge Regularization

Ridge Regularization, also known as L2 regularization, adds a penalty equal to the square of the weights associated with each feature variable.

This encourages all coefficients to reduce in size by an amount proportional to their values and reduces model complexity by shrinking large weights toward zero.

Ridge regularization can be more effective than Lasso when there are many collinear variables because it prevents individual coefficients from becoming too large and overwhelming others.

Lasso and Ridge regularization can both be used together to combine the advantages of each technique. The combination is known as elastic net regularization and can produce simpler models while still utilizing most or all of the available features.

It has become increasingly popular in machine learning due to its capability to improve prediction accuracy while minimizing overfitting. 

However, when comparing Lasso vs. Ridge regularization, we see Ridge regularization can produce more complex models with better prediction power. Still, we may suffer from overfitting due to its reliance on all available features.

In comparison, Lasso regularization can reduce the number of features used in a model and eliminate noisy ones while producing simpler models that are more likely to generalize.

How to Perform Ridge and Lasso Regression in Python

We will use the popular `scikit-learn` library to implement Ridge and Lasso Regression in Python.

Step 1: Ensure that you have the library installed:

pip install scikit-learn

Then, you can import the necessary libraries and load a sample dataset:  

Next, you can split the dataset into train and test sets and instantiate both Ridge and Lasso models:

Finally, you can fit the models on the training set and evaluate their performance on the test set:

You can then compare the predictions of both models against actual values to evaluate their performance and determine which model is more suitable for our problem.

In conclusion:

• Lasso and Ridge Regression are two popular regularization techniques used to prevent overfitting and improve the accuracy of linear Regression models.
• While both methods aim to reduce coefficients’ magnitudes, they differ in terms of how they do so – Lasso uses L1 regularization while Ridge uses L2 regularization. 
• Furthermore, Lasso can force certain features’ coefficients to be zero, thus performing feature selection alongside regularization, while Ridge does not.
• Both methods should be tuned using cross-validation for optimal results.
• Lastly, it is important to consider which technique is more suitable for a given problem since some scenarios require one approach over the other.

Limitations of Ridge and Lasso Regressions

Ridge and Lasso Regression are powerful techniques for predicting continuous and categorical outcomes. However, they have their limitations as well.

• The Ridge-Lasso approach is limited in requiring the input features to be standardized before fitting the model. It means that any feature with a large range of values can bias results because of its scale relative to other features with smaller ranges.
• Furthermore, if the data points contain outliers or noise, then this could produce inaccurate predictions due to the penalty terms.
• Additionally, Ridge and Lasso Regressions can be slow when applied to large datasets because of the computation time needed to perform regularization.
• Lastly, these methods require careful selection of hyperparameters (i.e., regularization strength), which can induce further computational costs and time.

Therefore, it is important to consider these limitations when deciding which model is best suited for a particular problem.

Use Cases of Lasso and Ridge

Lasso and Ridge Regression both add a penalty to the cost function used in linear Regression that reduces overfitting and provides better model interpretability.

Lasso and Ridge can be used in many different scenarios, such as predicting stock prices or estimating housing costs.

• Finance

In finance, Lasso is especially useful for feature selection on large data sets because it can effectively reduce noise from irrelevant variables. Additionally, Lasso can be used to identify key drivers of returns by shrinking coefficients toward zero. This helps eliminate redundant variables from consideration while still accounting for nonlinear relationships between features.

• Predicting Outcomes

Ridge Regression is ideal for predicting outcomes when there are too many input variables, and multicollinearity is present. This technique can help reduce the effects of this by shrinking coefficients toward zero while still preserving their sign, allowing you to identify which inputs are most important for predicting an outcome.

Ridge Regression is also useful for predicting outcomes when there are outliers in the data, as it helps mitigate potential overfitting from these outliers by penalizing them less than other inputs.

Overall, Lasso and Ridge Regression can be used in many different scenarios. By applying a penalty on certain features or by reducing certain coefficients towards zero, they can provide more interpretable models with fewer input variables that still account for nonlinear relationships between inputs.

Conclusion

Lasso and Ridge Regression are two of the most popular techniques for regularizing linear models, which often yield more accurate predictions than traditional linear models. These methods reduce the model’s complexity by introducing shrinkage or adding a penalty to complex coefficients. 

Both have been successfully used in data science applications to help identify important features, reduce overfitting, and improve predictive performance. Ultimately, these techniques provide an invaluable tool for data scientists to use when tackling complex Regression problems.

FAQs:

• What is Lasso and Ridge Regression?

Lasso and Ridge Regression are two common methods of regularization used in machine learning. Regularization is the process of adding an additional constraint to the model to reduce the complexity of a given model by forcing certain predictor variables to have a smaller impact on the outcome or no effect at all.

• What is the Purpose of Lasso Regression?

The purpose of Lasso Regression is to help with feature selection and reduce the complexity of a model. It does this by regularizing the coefficients of each predictor variable, meaning it penalizes large coefficient values to bring them down to a size that is more manageable. This helps overall model accuracy by reducing the number of variables used while improving predictive power. 

Lasso Regression also works well for datasets with high multicollinearity levels (when two or more predictor variables are highly correlated). Finally, Lasso Regression can be useful for data sets with large numbers of predictors, as it can quickly determine which variables are most important and eliminate those that do not contribute much information.

• What is the Main Advantage of Ridge Regression and Lasso Regression?

The main advantage of Lasso and Ridge Regression is that both techniques reduce the complexity of a model by penalizing high coefficients, making them useful for feature selection.

Ridge Regression adds an L2 regularization term, which shrinks coefficient values but does not set any coefficient to zero. In other words, it helps control overfitting by reducing the magnitude of coefficients while still keeping all predictors in the model.

On the other hand, Lasso Regression adds an L1 regularization term, which can set the coefficient of some predictors to zero, effectively eliminating them from the model. This helps to reduce complexity further and improve interpretability by reducing the number of variables included in a model.

Overall, both Ridge Regression and Lasso Regression offer advantages for feature selection that help reduce overfitting and improve interpretability.